问题定义

有 N 组物品和一个容量是 V 的背包。每组物品有若干个，同一组内的物品最多只能选一个。每件物品的体积是 vij，价值是 wij，其中 i 是组号，j是组内编号。求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。输出最大价值。

事实上是在01背包的问题上增加条件:第i组有k个物品,每组只能选一个.

状态分析

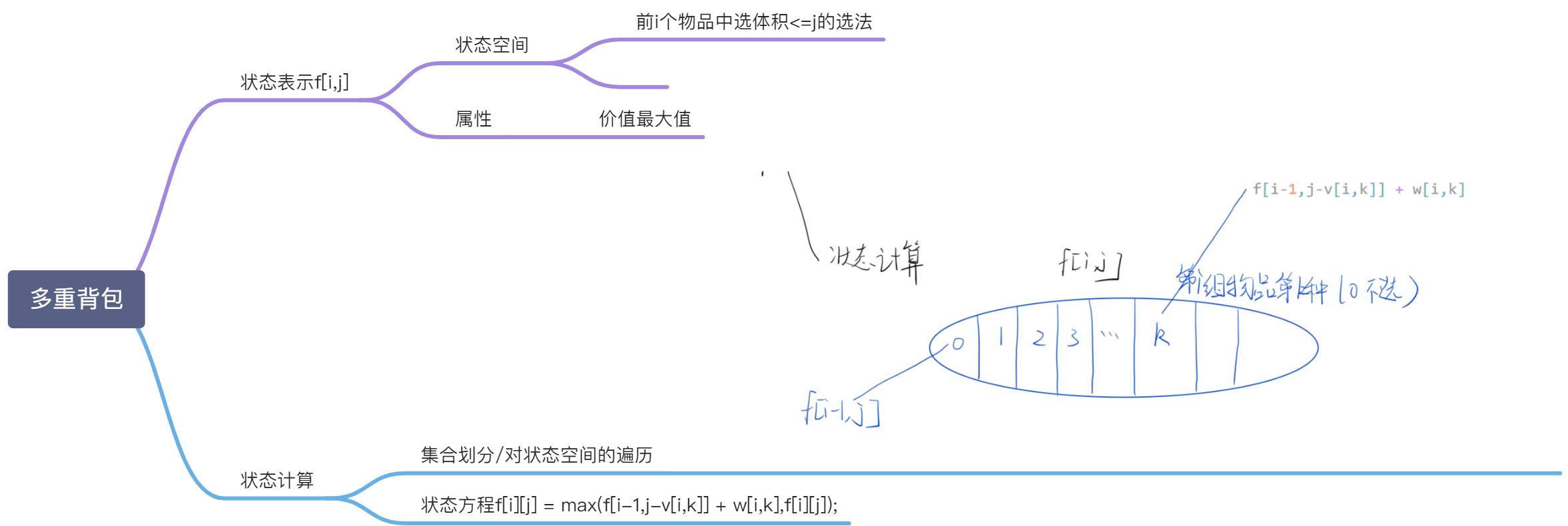
思路

• 前i个物品不超过j的最大价值=max(当前价值,取i组物品的第k个物品的价值+i组第k个物品的价值)
• 注意实际实现的过程中第i组第k个物品不一定能取,因为体积可能会不够.
• 本质上问题抽象成状态空间,通过状态转移来计算
• 可以滚动数组优化

详细注释代码I

/*
 * @Author: ACCXavier
 * @Date: 2021-04-28 22:48:06
 * @LastEditTime: 2021-04-28 23:07:55
 * Bilibili:https://space.bilibili.com/7469540
 * 题目地址:https://www.acwing.com/problem/content/description/9/
 * @keywords: 分组背包
 * 
 */
#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 110;
int f[N], v[N][N], w[N][N], s[N];
int n, m;
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        cin >> s[i];
        for (int j = 1; j <= s[i]; ++j) {//@1从1开始,第i组物品的第j种
            cin >> v[i][j] >> w[i][j];
        }
    }
    for (int i = 1; i <= n; ++i) {
        for (int j = m; j >= 0; --j) {
            for (int k = 0; k <= s[i]; ++k) {//能够遍历到=s[i]是因为@1处下标从1开始,第s[i]种的下标就是s[i],如果@1处从0开始则这里k不能取到s[i]//另外,不拿第i组等价于f[j] = f[j],所以这里k取1和0都可以
                if (v[i][k] <= j) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);//@v[i][k] 第i组的第k种 不是v[i][j]
            }
        }
    }
    cout << f[m];

    return 0;
}