分析题意可得：

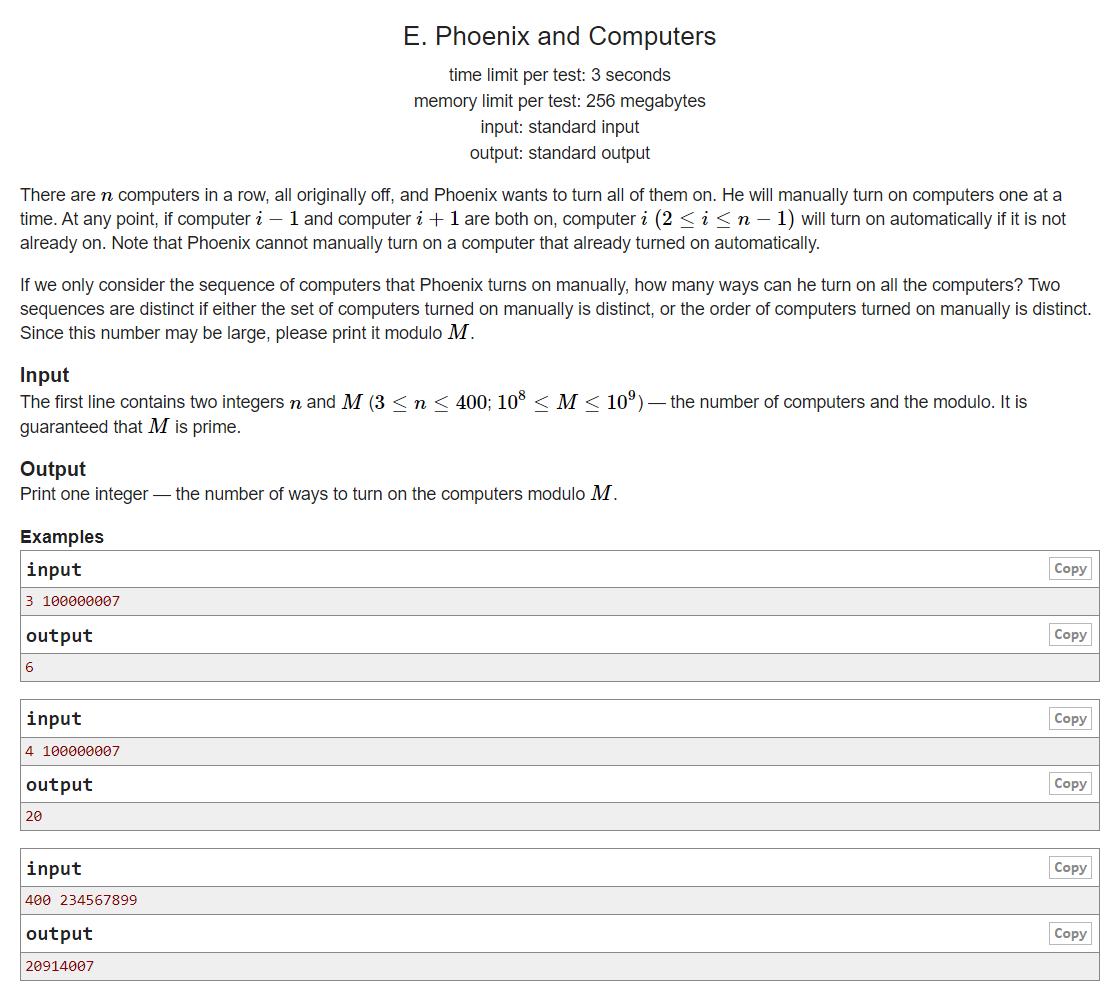
• 标记手动打开的电脑为1，自动打开的电脑为0，最终状态必然形如：110111011，即若干个1后伴随一个0。（最后无0）

这里引入一个量：$g[k]=2^{k-1}$($k$台手动启动的电脑开启的方案数)。因为不存在自动开启的电脑，因此每次开机只能从所有已开启的电脑的两侧打开，于是每次开机有左右两次选择，即$g[k]=g[k-1]*2$，又因为一台电脑的打开方案数$g[1]=1$，因此$g[k]=2^{k-1}$。

状态表示

显然若直接设置$f[i]$表示打开i台电脑的方案数是不合理（为涉及自动开启的情况）

因此想到设$f[i][j]$表示一共$i$台电脑被打开，其中$j$台是手动打开的方案数。

状态转移

这里采用由己推人的转移方式，若当前的状态的为$f[i][j]$，我们可以枚举添加的手动改开机的电脑台数$k$，那么转移到的状态应该是$f[i + k + 1][j + k]$，因为若个$1$必然伴随一个$0$，所以第一维的状态要加上$1$。

考虑转移方程：如何将$k$手动开机的电脑插入已有的状态？
因为现在已有$j$手动开启的电脑，那么根据组合计数，若再插入k台，那么方案数应该是$C_{j+k}^{k}$，又因为手动开启$k$台电脑的方案数是$g[k]=2^{k-1}$，那么转移方程可得:$$f[i+k+1][j+k]= \sum_{k=1}^{n-i} f[i][j] * g[k-1] * C[j+k][k]$$

最终答案
最后还要考虑一下答案的表示，因为之前插入手动开启电脑时都伴随了一个自动开启的电脑，但实际情况中最后一个$0$并不会存在因此在计算答案时要考虑上最后一个$0$，即多加一台电脑，因此：$$res = \sum_{i=0}^{n}f[n+1][i]$$

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 410;

LL f[N][N] , n , P;
LL C[N][N] , g[N];

//预处理
void init()
{
    g[0] = 1;
    for(int i = 1 ; i < N ; i++) g[i] = g[i - 1] * 2 % P;

    for(int i = 0 ; i < N ; i++)
        for(int j = 0 ; j <= i ; j++)
            if(!j) C[i][j] = 1;
            else C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % P;
}

int main()
{
    cin >> n >> P;

    init();

    //初始时从实际出发如果没有电脑，那么0台手动启动的方案数是1
    f[0][0] = 1;
    for(int i = 0 ; i < n ; i++)
        for(int j = 0 ; j <= i ; j++)
            for(int k = 1 ; k + i <= n ; k++)//枚举加入手动开启的电脑的数量
            {
                f[i + k + 1][j + k] += f[i][j] * g[k - 1] % P * C[j + k][k] % P;
                f[i + k + 1][j + k] %= P;
            }

    LL res = 0;
    for(int i = 0 ; i <= n ; i++) res = (res + f[n + 1][i]) % P;

    cout << res << endl;
}