算法:栈 + 找规律

这题也是思维题，赛后找规律才找出来，不需要用线段树或者 $Splay$，只用一个栈也可以写
如果暴力用 $sort$ 的话会超时
假设这是我们的原序列

优化一： 由于一开始的序列是升序的，所以如果一开始的操作是后缀操作的话是没有意义的，序列是不会改变的，所以我们从前缀操作开始看，红色为将要操作的前缀序列

如果有连续的前缀操作，我们发现只需要进行最长的一个前缀操作即可，因为短的前缀操作后，长的还是要进行操作，为何不直接进行最长的前缀操作呢，后缀操作同理，我们把所有的操作节点存进栈，有两个成员变量，一个是当前操作是前缀操作还是后缀操作，另一个是操作的边界

优化二： 若进行到下图这种情况时

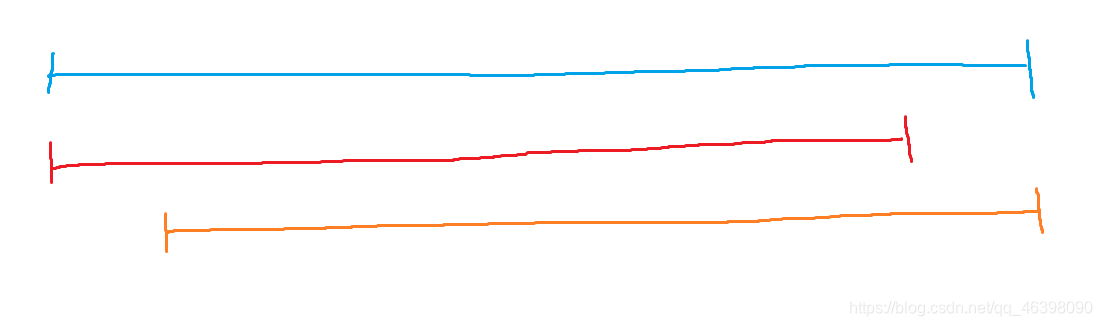
蓝色为原序列，红色为最长连续前缀，橙色为最长连续后缀

从下图我们发现
- 原序列 $A$ 段严格大于 $B$ 段
- $A$ 段 $=$ $A_{1}$ 段， $B$ 段 $=$ $B_{1}$ 段
- 所以 $A_{1}$ 段严格大于 $B_{1}$ 段
- $A_{2}$ 段 $=$ $A_{1}$ 段
- 所以 $A_{2}$ 段严格大于 $C$ 段，所以后缀升序操作（橙色）只需要操作 $C$ 段即可

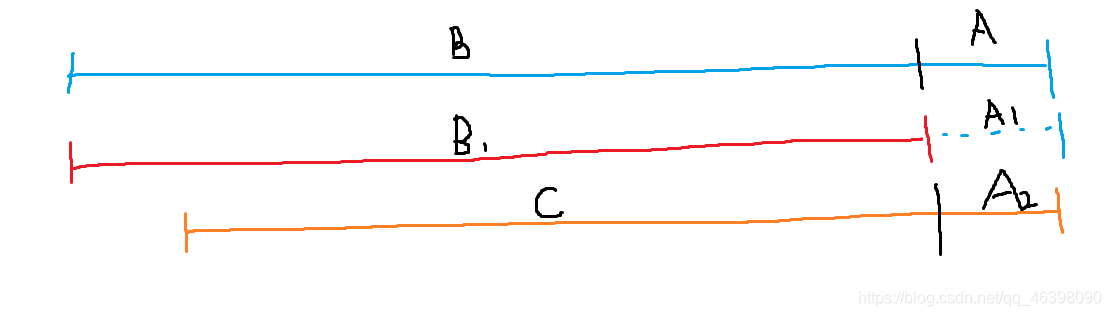
对于前缀操作同理 ，只需要操作 $C$ 段即可

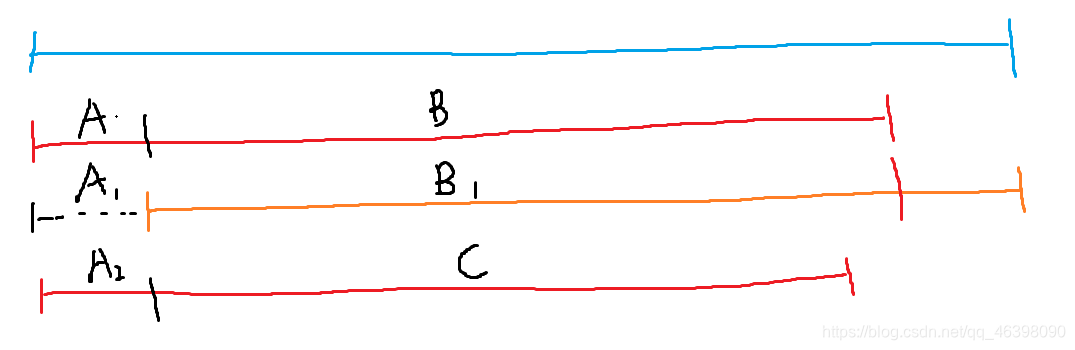
优化三： 当出现下面这种情况时

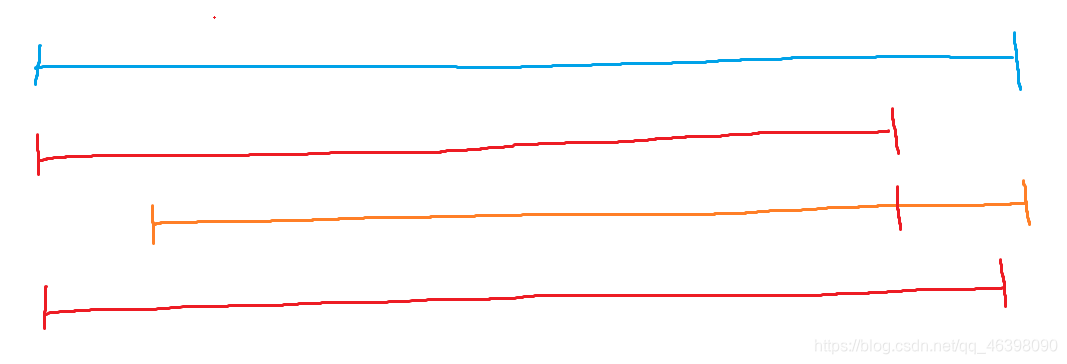
也就是在进行一次前缀操作和后缀操作后，下一次的前缀操作在上一次的前缀操作的节点后，这个时候我们可以把前两次操作给删去，直接进行这一次的前缀操作，因为上一次的后缀操作和前缀操作都包含在了这一次的前缀操作内，前两次操作等于是没用的，所以我们只需要保留当前操作即可

另外，我们可以发现在我们一次次操作的过程中，操作的区间是在慢慢变小的，每次操作的时候，序列总有一部分是不需要进行操作的，我们也就可以用一个变量来递减的填入数组中

代码：

import java.util.Scanner;

public class Main {

    static int N = 100010;
    static int n, m;
    static PII[] stk = new PII[N];
    static int[] ans = new int[N];
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();
        int top = 0;//栈顶

        while (m -- > 0) {

            int p = sc.nextInt();
            int q = sc.nextInt();

            if (p == 0) {
                //求出连续操作的最长前缀
                while (top != 0 && stk[top].x == 0) q = Math.max(q, stk[top -- ].y);
                //优化三
                while (top >= 2 && stk[top - 1].y <= q) top -= 2;
                stk[ ++ top] = new PII(0, q);
            } else if (top != 0) {
                //求出连续操作的最长后缀
                while (top != 0 && stk[top].x == 1) q = Math.min(q, stk[top --].y);
                //优化三
                while (top >= 2 && stk[top - 1].y >= q) top -= 2;
                stk[ ++ top] = new PII(1, q);
            }
        }

        //k是递减变量，l为左边界，r为右边界
        int k = n, l = 1, r = n;
        for (int i = 1; i <= top; i ++ ) {
            if (stk[i].x == 0) {
                //若为前缀操作，则(stk[i].y, r]不用操作，直接填数
                while (r > stk[i].y && l <= r) ans[r -- ] = k --;
            } else {
                //若为后缀操作，则[l, stk[i].y)不用操作，直接填数
                while (l < stk[i].y && l <= r) ans[l ++ ] = k --;
            }
            if (l > r) break;
        }

        //若l < r, 表示中间还有些数没有填上，操作次数为奇数，则下一次操作为前缀操作
        if (top % 2 == 1) {
            while (l <= r) ans[l ++ ] = k --;
        } else {
            while (l <= r) ans[r -- ] = k --;
        }

        for (int i = 1; i <= n; i ++ ) System.out.print(ans[i] + " ");
    }

    static class PII {
        int x, y;

        public PII(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }

}