题目描述

给定一个非空数组：$a_0, a_1, … a_{n - 1}$，其中 $0 \le a_i \lt 2^{31}$。

请计算 $a_i$ XOR $a_j$ 的最大值，其中 $0 \le i, j \lt n$。

你可以只使用 $O(n)$ 的时间吗？

样例

输入：[3, 10, 5, 25, 2, 8]

输出：28

解释：最大的结果是 5 ^ 25 = 28.

算法

(Trie，位运算) $O(n)$

我们把每个数的二进制表示看成字符串，然后用Trie树给这些数建立索引。

以样例[3, 10, 5, 25, 2, 8]为例，建完树之后可以得到下图：

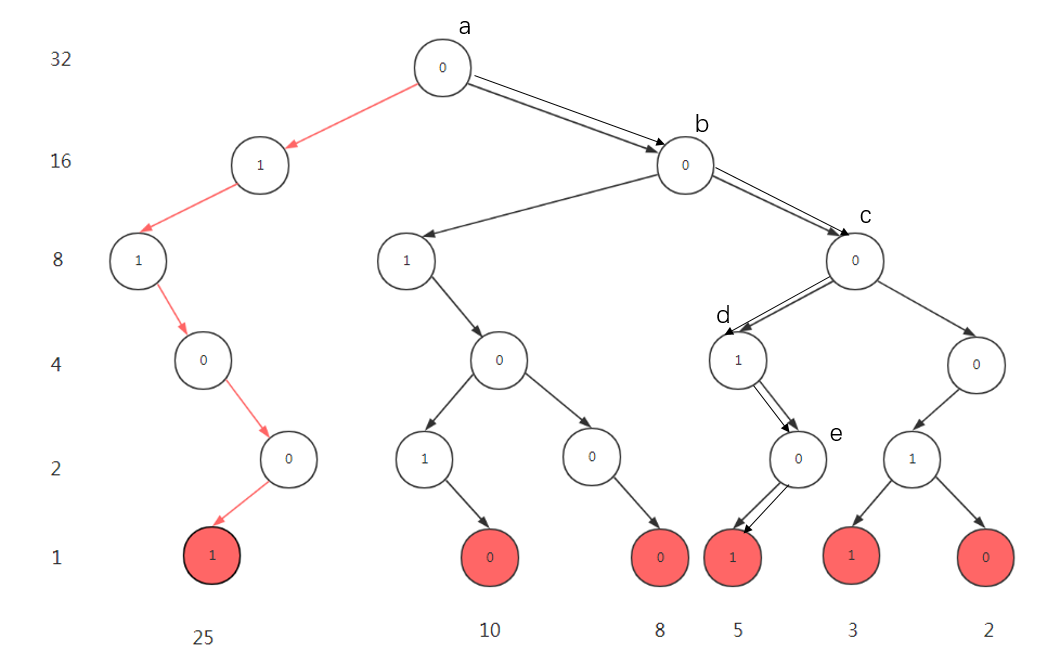
左儿子为1的分支，右儿子为0的分支。

然后依次枚举每个数，在Trie树中找到与它异或结果最大的数。
这一步可以贪心来做：
从高位到低位，依次在Trie树中遍历，每次尽量走到与当前位不同的分支，这样可以使得找到的数与当前数在当前二进制位的异或结果是1，从而可以得到尽量大的结果。

如上图所示，我们用25来举例说明，它的二进制表示是(11001)：

1. 最初指针在根节点(编号是a的点)，我们从25的二进制表示的最高位开始枚举；
2. 由于最高位是1，我们走到0分支，走到b点；
3. 次高位是1，我们继续往右儿子走，走到c点；
4. 下一位是0，我们往左走，走到d点；
5. 下一位是0，我们希望往左走，但发现左儿子不存在，所以只能往右走，走到e点；
6. 最后一位是1，我们希望往右走，但发现右儿子不存在，所以只能往左走，最终走到5；

所以和25异或值最大的数是5, 25 ^ 5 = 28。

接下来的问题，就是如何建立Trie树了。
我们可以使用一种比较简洁的方式：
建树的过程，本质上就是构建节点与节点之间边的过程。这里我们可以用哈希表来存储Trie树的所有边。

假设当前节点是 p，我们用一个long long变量来存储当前边的哈希值。
哈希函数可以随意发挥，只要保证冲突的概率很小即可。这里我使用了一种完全不会冲突的哈希函数：

long long变量的低32位存储p点到根节点的路径所表示的二进制数，第32位存储当前边是0还是1, 从第33位开始，表示节点p的高度。

例如，假设p点到根节点的前缀是$(101)_2 = 5$，当前边是1，p在Trie树中的高度是27，则当前边的哈希值是：
$$ 5 + 1 * 2^{32} + 27 * 2^{33} $$

时间复杂度分析：对于每个数，我们会将其在Trie树中插入一次，然后再在Trie树中查询一次。插入和查询的计算量和树的高度成正比，int最多有32位，所以Trie树的高度最多是32。所以总时间复杂度是 $O(2 * 32 n) = O(n)$。

C++ 代码

class Solution {
public:
    typedef long long LL;

    int findMaximumXOR(vector<int>& nums) {
        unordered_set<LL> edge;
        int res = 0;
        for (auto &x : nums)
        {
            LL pre = 0, pre_op = 0;
            int xorr = 0;
            for (int i = 30; i >= 0; i--)
            {
                int next = x >> i & 1;
                edge.insert(pre + next * (1LL << 32) + i * (1LL << 33));
                if (edge.count(pre_op + !next * (1LL << 32) + i * (1LL << 33)))
                {
                    xorr = xorr * 2 + 1;
                    pre_op = pre_op * 2 + !next;
                }
                else
                {
                    xorr <<= 1;
                    pre_op = pre_op * 2 + next;
                }
                pre = pre * 2 + next;
            }
            res = max(res, xorr);
        }
        return res;
    }
};