题目描述
两位玩家分别扮演猫和老鼠,在一张 无向 图上进行游戏,两人轮流行动。
图的形式是:graph[a] 是一个列表,由满足 ab 是图中的一条边的所有节点 b 组成。
老鼠从节点 1 开始,第一个出发;猫从节点 2 开始,第二个出发。在节点 0 处有一个洞。
在每个玩家的行动中,他们 必须 沿着图中与所在当前位置连通的一条边移动。例如,如果老鼠在节点 1 ,那么它必须移动到 graph[1] 中的任一节点。
此外,猫无法移动到洞中(节点 0)。
然后,游戏在出现以下三种情形之一时结束:
- 如果猫和老鼠出现在同一个节点,猫获胜。
- 如果老鼠到达洞中,老鼠获胜。
- 如果某一位置重复出现(即,玩家的位置和移动顺序都与上一次行动相同),游戏平局。
给你一张图 graph,并假设两位玩家都都以最佳状态参与游戏:
- 如果老鼠获胜,则返回
1; - 如果猫获胜,则返回
2; - 如果平局,则返回
0。
样例
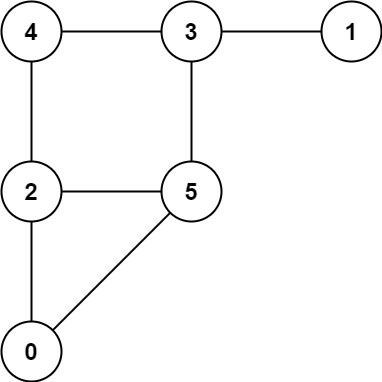
输入:graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]]
输出:0
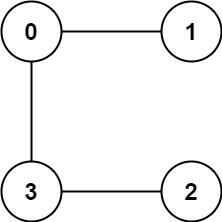
输入:graph = [[1,3],[0],[3],[0,2]]
输出:1
注意
3 <= graph.length <= 501 <= graph[i].length < graph.length0 <= graph[i][j] < graph.lengthgraph[i][j] != igraph[i]互不相同。- 猫和老鼠在游戏中总是移动。
算法
(动态规划) $O(n^3)$
- 从结果开始倒推起始点的值。设 $f(i, j, t)$ 表示老鼠在 $i$,猫在 $j$,当前下一步轮到 $t$ 行动时,最终的结果。其中,$t=0$ 表示下一步老鼠移动,$t=1$ 表示下一步猫移动。
- 已经确定的初始值,$f(0, i) = 1$,$f(i, i) = 2$,其余为 $0$ 待定。将已经确定的状态加入队列,按照拓扑顺序进行动态规划的转移。队列里只存储可以完全确定老鼠获胜或者猫获胜的状态,不考虑平局的未知状态。
- 如果当前状态是老鼠移动,且是猫获胜,则上一步猫移动时,则必定会走到这个猫必胜的状态,所以所有相连的上一步的猫状态为猫必胜,且进队。如果当前状态是老鼠获胜,且某个的上一步的状态的所有其他(下一步)的状态都是老鼠获胜,则其上一步的状态也是老鼠获胜(可以通过 deg 数组判断),且进队。
- 同理,当前状态是猫移动时,对偶处理。
- 最终,进过队列的状态都是确定结局的状态,不确定结局的状态都是平局。
- 最终 $f(1, 2, 0)$ 的值为答案。
时间复杂度
- 遍历的节点数量为 $O(n^2)$,每个点拓展的时间复杂度为 $O(n)$,故总时间复杂度为 $O(n^3)$。
空间复杂度
- 需要 $O(n^2)$ 的额外空间存储状态和队列。
C++ 代码
const int N = 51;
class Solution {
private:
int f[N][N][2], deg[N][N][2];
public:
int catMouseGame(vector<vector<int>>& graph) {
const int n = graph.size();
memset(f, 0, sizeof(f));
for (int i = 0; i < n; i++)
for (int j = 1; j < n; j++) {
deg[i][j][0] = graph[i].size();
deg[i][j][1] = graph[j].size();
}
for (int i = 0; i < n; i++)
for (int v : graph[0])
deg[i][v][1]--;
queue<vector<int>> q;
for (int j = 1; j < n; j++) {
f[0][j][0] = f[0][j][1] = 1;
q.push({0, j, 0});
q.push({0, j, 1});
}
for (int i = 1; i < n; i++) {
f[i][i][0] = f[i][i][1] = 2;
q.push({i, i, 1});
q.push({i, i, 0});
}
while (!q.empty()) {
auto u = q.front();
q.pop();
int i = u[0], j = u[1], t = u[2];
if (i == 1 && j == 2 && t == 0)
break;
if (t == 0) {
for (int v : graph[j]) {
if (v == 0)
continue;
if (f[i][v][1] != 0)
continue;
if (f[i][j][t] == 2) {
f[i][v][1] = 2;
q.push({i, v, 1});
} else {
deg[i][v][1]--;
if (deg[i][v][1] == 0) {
f[i][v][1] = 1;
q.push({i, v, 1});
}
}
}
} else {
for (int v : graph[i]) {
if (f[v][j][0] != 0)
continue;
if (f[i][j][t] == 1) {
f[v][j][0] = 1;
q.push({v, j, 0});
} else {
deg[v][j][0]--;
if (deg[v][j][0] == 0) {
f[v][j][0] = 2;
q.push({v, j, 0});
}
}
}
}
}
return f[1][2][0];
}
};


记忆化搜索已改为拓扑排序的动态规划。因为记忆化搜索不能使用 $2n$,只能用 $2n^2$ 来判断平局,会 TLE
我觉得超过 2n time 就表明 draw 了可以这么证明:老鼠至多 n - 1 步就可以到达 0,我们记从 1 到 0 的这条路径为 path. 如果第 n 步老鼠没有到达 0 的话,就说明在某个时刻,老鼠偏离了原本的路径 path, 为什么会偏移呢?说明在前面的某一点 p,猫在旁边候着。猫到点 p 的距离小于等于老鼠到点 p 的距离。(注意可以有多个这样的点 p, 无论老鼠选取那条通往 0 的路径,路上都有一个这样的点,老鼠会在这个点被猫逮到)。而老鼠不经过 p 的话又不可能到达 0。
这可不叫证明
这题f[t][x][y]可不可用滚动数组对t模2?试了一下个别test case不过。请问什么地方需要注意?
滚动数组一般不能用到记忆化搜索的DP中,因为每一层的状态都需要记录,和循环实现的DP有一些区别。
是的。这个题每次递归只从t到t+1,我就试了一下。极个别情况会fail。
首先
if (t == graph.size() + 1)
这一句应该是
if (t == graph.size() * 2)
因为老鼠走n步,猫也走n步,加起来是2n步,对于你现在的程序,反例特别简单,
3-2-0-4-5-6-7-8-9-1
按照这个图,猫只能来回走,老鼠7步可以走到0,总计13步后老鼠获胜
第二,你所说的老鼠或者猫如果回到之前走过的位置就一定是平局,这个结论明显是错的,上面本身就是一个反例,而且构造一个猫和老鼠所在位置连通的反例也很容易,但奇妙的是,我构造出的所有反例,都能在2n步以内得到结果,极限步数趋向于2n,所以我现在倾向于认为这个游戏只要超过2n步就可以判定为平局,但是我证明不了。
最后@2018coder,这个问题如果用传统的dfs,存在一个结果正确的做法,但是结果正确的做法为了遍历所有的可能,在大数据里一定会栈溢出。
我感觉里面dfs的过程中循环了,本身没有其他办法退出循环,
我的例子里面就是在这个状态里面不停的循环, 把状态的第一个节点改成level了以后只是遇到level超出了以后才退出循环, 即使是2n, 我认为也是不改变逻辑,只是循环的次数变多了而已
我提出的是两个完全不同的方案。
1. 证明如果不是平局,一定能在2n步之内获得一个解,是不是循环跟我们就没有任何关系了,唯一的问题是证明比较困难。
2. 传统的dfs不停的循环并非没有解决方案,你只要对于每个状态加标记,记录以前走过的路,之后再也不走就可以了,唯一的问题是这是无向图,在n比较大的时候我们遍历所有的状态会导致栈溢出。
如果答案不是draw,dfs在n^2步内一定能找到解,因为dfs会在n^2步内枚举到所有可能的位置。
既然 n 步已经被否决了,那可以试着找下 2n 的反例。
我貌似忽略了这点,应该是2n。我先暂时把upper_bound改到2n吧,n^2会导致MLE。
你好,能不能请教一下为什么需要每个level存一个状态? 虽然我想每个level存一个状态的好处是在一条递归路径上后面的结果不会被前面的影响, 也就是遇到重复节点的时候可以避免这个节点的结果还没有算出来就直接因为重复就判draw了,
但是我理解是
1. [turn, mousepos, catpos]就决定了这个状态节点的值,和他在哪个level没有关系,
2. 对于每个节点,只要我们遍历了所有的邻居节点以后再最后决定他的值,应该就可以得出正确的结果
但是我用下面的代码就会出错,
能指点一下嘛?
谢谢
我尝试了只用这样的状态,会出错。我感觉原因在于这样的状态表示,DP会出现环;但这里出现环并不一定就是draw,可能环里有其他的出口能到达一个确定的状态。
谢谢, 对,dp出现环确实是不同的地方,但是困惑的是感觉下面这两步逻辑并没有问题
1. [turn, mousepos, catpos]就决定了这个状态节点的值,和他在哪个level没有关系,
2. 对于每个节点,只要我们遍历了所有的邻居节点以后再最后决定他的值,应该就可以得出正确的结果。 这里就算出现了环(访问到dfs前面已经访问的结果,但是这部分子树还没有搜索完), 但是对于任何一个节点,仍然只会在所有邻居节点全部都尝试了以后才会设置值,不知道那里错了。。。
Check this case:
[[6],[4],[9],[5],[1,5],[3,4,6],[0,5,10],[8,9,10],[7],[2,7],[6,7]]
用自底向上从两个出口往回递推应该是没有问题的,但用记忆化搜索就会出问题,因为记忆化搜索遇到环且不规定环的出口会死循环,但递推总会从出口往回找,遇到环可以直接宣布平局。
谢谢!
我又debug了一下这组数据, 大概明白了为什么我改的代码是错的,原因是部分递归过程, dp表格出现了环, 不停的在环里面循环, 直到深度超出了,然后判和退出。 递归过程如下, 这里level=12的两个步骤,都是因为深度超出了,才导致判和。虽然在这个过程中,对于level在11遇到的(cat,1,9)这个状态节点,所有子节点都尝试了,但是因为尝试的过程受到前面在环里面不停循环的影响,导致深度超过了, 所以每个节点的判断都是不准确的,因为对于一个环上的节点,由于循环的存在,[turn,mousepos,catpos]本身的值已经不再能通过深度超出来判和了,相当于前面的循环导致后续判断其他节点的值不准确了。
我有一个问题,感觉你的代码用[level,mousepos,catpos]做状态似乎也没有解决环的问题,只是减少了错误的可能性,因为[level,mousepos,catpos]被错误利用的可能性大大减小了,至少在一次递归的过程中是不会被错误利用的,而在其他情况下正好遇上那个错误的[level,mousepos,catpos]的可能性小了很多,但是还是有可能会存在同样的错误值。
虽然我构造不出来一组数据可以验证这个,你决定这个猜想成立嘛? 是不是这个问题其实dfs无法解决重复环的问题?
最保守的 level 是取 $n^2$,因为最多只有 $n^2$ 的状态可以到达,如果都尝试了就只能平局。但这里我取的 $n$ 实际上是基于一个贪心,如果老鼠或者猫走的路径出现的重复结点,说明已经在向对方妥协了。
其实我的问题倒不是level高度不够,而是[level,mousepos,catpos]在递归过程中也会得到错误的值,并且可能被错误利用? 只是这个被错误利用的概率比[turn,mousepos,catpos]的概率小很多很多。
本质上在同样的dfs代码下,[level,mousepos,catpos]和[turn,mousepos,catpos]导致错误的原因是一样的,都是因为环导致错误的状态被存在这个表里面,只是[level,mousepos,catpos]被撞上的概率很小
[level,mousepos,catpos]在递归过程中应该不会得到错误的值,层数够深有环就是draw了
{{6},{4},{9},{5},{1,5},{3,4,6},{0,5,10},{8,9,10},{7},{2,7},{6,7}}
比如针对上面的case, 下面是我debug的递归过程,最后那几行看到的状态都是不对的
这只是递归的一条分支,但老鼠在某一层有其他的走法,这样能到达终点,所以就能正确更新
主要的问题在于, 其他走法被level超出影响了, 然后直接判draw了, 没有继续往后面走
我感觉,f 的初始化长度可以是n,不用n+1。if (t == graph.size() + 1)return 0;这里不用加1
是的