题目描述

给定一个 $m \times n$ 的矩阵，其中的值均为正整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

说明

$m$ 和 $n$ 都是小于110的整数。每一个单位的高度都大于 0 且小于 20000。

样例

给出如下 3x6 的高度图:
[
  [1,4,3,1,3,2],
  [3,2,1,3,2,4],
  [2,3,3,2,3,1]
]

返回 4。

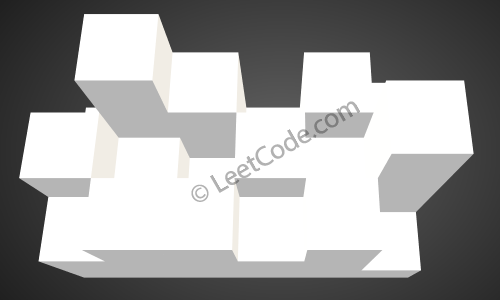
如上图所示，这是下雨前的高度图[[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] 的状态。

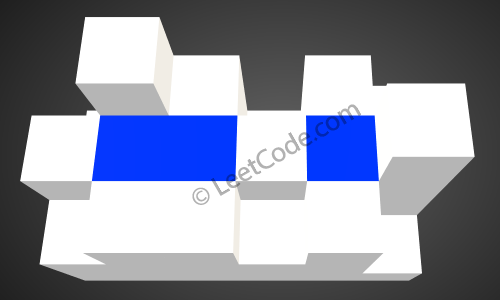
下雨后，雨水将会被存储在这些方块中。总的接雨水量是4。

算法

(堆) $O(m\times n\log mn)$

这里思路类似于 LeetCode 42. Trapping Rain Water 中的双指针算法，但不完全相同。如果对于每个点我们找到其上下左右四个方向的最大值，然后用当中的最小值减去当前柱子的高度来得到该点的盛水量，这样得到的答案是错误的，原因在于从该点开始可能存在一条高度递减的路径使得水流出边界外，即四个方向上的最大值并不能保证“包围”住该点。所以这里我们同样需要维护边界，但这里的边界变成了边而不是点。每次我们需要找到边界里的最小值，然后计算水的高度以及维护边界。动态的维护一堆点的最小值我们可以用堆来实现。

初始时我们先将上下左右四条边的点插入最小堆中，然后每次弹出最小值，那么对于最小值的邻近上下左右四个点来说，如果它比最小值还小，那么这个柱子就可以盛体积为它们高度差的水，然后我们将这个点加入堆中。注意这里插入的高度为当前点与最小值点的最大值，因为我们要维护的是边界，如果插入的是较小值那么对于下一个点来说计算出来的水会变少。另外为了避免一个点被重复的插入堆中，我们额外开一个数组记录每个点是否被访问过。

通过上述过程我们可以保证对于每个可以盛水的柱子，该做法得到的盛水量是该点能盛水的最大值，即如果再多盛水则水就会流出边界外（因为从当前最小值点一定存在一条到容器外的递减路径），而且当前盛的水恰好不会流出边界外（因为从当前点不存在一条到容器外的递减路径）。

时间复杂度

每个点只会插入弹出堆一次，总共有$m \times n$个点，每次插入与弹出最多需要$O(\log mn)$的时间，因此总时间复杂度为$O(m\times n\log mn)$。

C++ 代码

class Solution {
public:
    struct Cell
    {
        int x, y, h;
        bool operator< (const Cell& c) const
        {
            return h > c.h;
        }
    };

    int trapRainWater(vector<vector<int>>& heightMap) {
        if (heightMap.empty() || heightMap[0].empty()) return 0;
        priority_queue<Cell> heap;
        int m = heightMap.size(), n = heightMap[0].size();
        vector<vector<bool>> st(m, vector<bool>(n));
        for (int i = 0; i < n; i ++ )
        {
            heap.push({0, i, heightMap[0][i]});
            heap.push({m - 1, i, heightMap[m - 1][i]});
            st[0][i] = st[m - 1][i] = true;
        }
        for (int i = 1; i < m - 1; i ++ )
        {
            heap.push({i, 0, heightMap[i][0]});
            heap.push({i, n - 1, heightMap[i][n - 1]});
            st[i][0] = st[i][n - 1] = true;
        }

        int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

        int res = 0;
        while (!heap.empty())
        {
            auto t = heap.top();
            heap.pop();

            for (int i = 0; i < 4; i ++ )
            {
                int a = t.x + dx[i], b = t.y + dy[i];
                if (a >= 0 && a < m && b >= 0 && b < n && !st[a][b])
                {
                    st[a][b] = true;
                    if (heightMap[a][b] < t.h) res += t.h - heightMap[a][b];
                    heap.push({a, b, max(t.h, heightMap[a][b])});
                }
            }
        }
        return res;
    }
};