题目描述

在一个R行C列的二维网格中，从(r0, c0)面向东的方向出发。

在这里，网格的西北角是第一行和第一列，网格的东南角是最后一行和最后一列。我们按照顺时钟螺旋顺序访问网格的每个位置。一旦我们走出了网格的边界，我们继续按照原来的路线走并且之后会回到网格的边界。

最好，我们会走遍网格的每一个格点。返回我们访问的网格格点的顺序列表。

样例

输入: R = 5, C = 6, r0 = 1, c0 = 4
输出: [[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]
说明：如下图

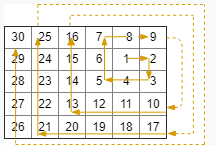
算法

$O(max(M,N)^2)$

按照顺序，先向右走，再向下走，再向左走，再向上走，经观察发现每个方向的步数依次为1,1,2,2,3,3,…，依次类推，按照步骤走即可，发现不在网格内就跳过。

时间复杂度分析：由于只能沿着正方形来走，于是复杂度为$O(max(M,N)^2)$

C++ 代码

class Solution {
public:
 vector<vector<int>> spiralMatrixIII(int R, int C, int r, int c) {
        vector<vector<int>> res;
        res.push_back({r, c});
        int dr, dc;
        for (int n = 1; res.size() < R * C; n+=2) {
            dr = 0;//right
            dc = 1;
            for (int i = 0; i < n; i++) {
                r += dr;
                c += dc;
                if (0 <= r && r < R && 0 <= c && c < C)
                    res.push_back({r, c});
            }
            dr = 1;//down
            dc = 0;
            for (int i = 0; i < n; i++) {
                r += dr;
                c += dc;
                if (0 <= r && r < R && 0 <= c && c < C)
                    res.push_back({r, c});
            }
            dr = 0;//left
            dc = -1;
            for (int i = 0; i < n+1; i++) {
                r += dr;
                c += dc;
                if (0 <= r && r < R && 0 <= c && c < C)
                    res.push_back({r, c});
            }
            dr = -1;//up
            dc = 0;
            for (int i = 0; i < n+1; i++) {
                r += dr;
                c += dc;
                if (0 <= r && r < R && 0 <= c && c < C)
                    res.push_back({r, c});
            }
        }
        return res;
    }
};