题目链接： AcWing 1209 带分数

题意： 给定一个数$N$，问有多少组$a,b,c$满足$a+\dfrac bc=N$，且$a,b,c$三个数不重不漏地涵盖$1-9$这$9$个数字，输出总组数

解题思路：

• 暴力枚举出$9$个数的全排列，然后用一个长度为$9$的数组保存全排列的结果
• 从全排列的结果中用两重循环暴力分解出三段，形如下图，通过 $i,j$ 将一个排列分割，每段代表一个数
  
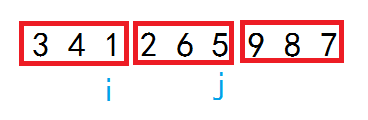
• 验证枚举出来的三个数是否满足题干条件，若满足则计数

代码如下：

#include <iostream>

using namespace std;

const int N = 10;

int target;  // 题目给出的目标数
int num[N];  // 保存全排列的结果
bool used[N];  // 生成全排列过程中标记是否使用过
int cnt;  // 计数，最后输出的结果

// 计算num数组中一段的数是多少
int calc(int l, int r) {
  int res = 0;
  for (int i = l; i <= r; i++) {
    res = res * 10 + num[i];
  }
  return res;
}

// 生成全排列
// 当全排列生成后进行分段
void dfs(int u) {
  // 用两层循环分成三段
  if (u == 9) {
    for (int i = 0; i < 7; i++) {
      for (int j = i + 1; j < 8; j++) {
        int a = calc(0, i);
        int b = calc(i + 1, j);
        int c = calc(j + 1, 8);
        // 注意判断条件，因为C++中除法是整除，所以要转化为加减乘来计算
        if (a * c + b == c * target) {
          cnt++;
        }
      }
    }
    return;
  }
  // 搜索模板
  for (int i = 1; i <= 9; i++) {
    if (!used[i]) {
      used[i] = true; // 标记使用
      num[u] = i;
      dfs(u + 1);
      used[i] = false; // 还原现场
    }
  }
}

int main() {
  scanf("%d", &target);
  dfs(0);
  printf("%d\n", cnt);
  return 0;
}

• UPD:2022-01-10
• 下面再给出一个直接调用 next_permutation() 函数的做法，可以代替手写暴搜来枚举全排列，蓝桥杯是可以使用这个函数的。
• 另外评论区下面很多初学的同学都比较疑惑循环边界问题，事实上像下面的代码一样，都写成全排列数组的个数（ $9$ ）也是一样的，只不过上面的代码在写的时候处理得更加细致一些，实际上没必要，像下面这么写就可以了。
• UPD:2022-03-04
• 之前的代码有点小问题，在判断时，需要将 $a,b,c$ 为 $0$ 的情况特判掉。

#include <bits/stdc++.h>

using namespace std;

const int N = 10;

int target;
int num[N];

int calc(int l, int r) {
  int res = 0;
  for (int i = l; i <= r; i++) {
    res = res * 10 + num[i];
  }
  return res;
}

int main() {
  cin >> target;
  for (int i = 0; i < 9; i++) {
    num[i] = i + 1;
  }
  int res = 0;
  do {
    for (int i = 0; i < 9; i++) {
      for (int j = i + 1; j < 9; j++) {
        int a = calc(0, i);
        int b = calc(i + 1, j);
        int c = calc(j + 1, 8);
        if (a == 0 || b == 0 || c == 0) {
          continue;
        }
        if (a * c + b == c * target) {
          ++res;
        }
      }
    }
    // 调用函数生成全排列
  } while (next_permutation(num, num + 9));
  cout << res << '\n';
  return 0;
}