思路

对于这种有依赖的背包问题，一般都是树形dp问题，要使用dfs递归完成。

分析一下题意，意思如果用了某一个物品，就必须用另一个和其相关的物品，利用这个特点，我们可以建立出一个树型结构，用邻接表来存下每一个物品之间的关系。

如何定义状态呢，这里想到用f[u][j]来表示以u为根节点的体积不大于j的解，下面我们再来看一下这个问题的模型
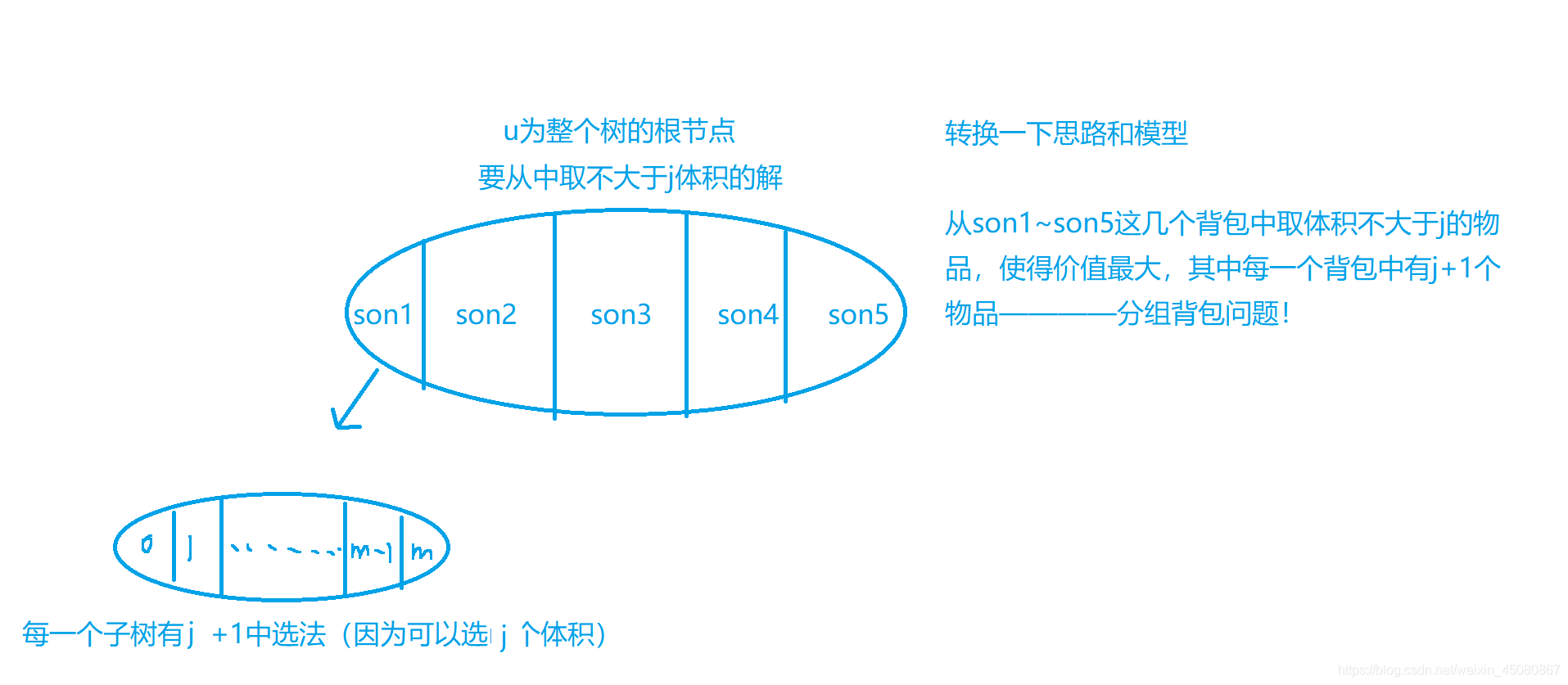这样就变成了一个分组背包问题

步骤：
1：创建邻接表，记录根节点

2：dfs遍历：

2.1：先判断如果连根节点都不能放入，就直接return
2.2：枚举子树，也就是相当于分组背包中的每一个背包
2.3：枚举体积
2.4：枚举每一个背包中的物品
2.5：因为以上是没有吧父节点的价值存入的，所以更新一下加入父节点的情况，如果能放入父节点就直接加入，不能就置为0

如果对于整个转移方程还是不懂的小伙伴，下面我写一下每一个集合代表的意义

f[u][j]=max(f[u][j],f[u][j-k]+f[son][k])

f[u][j]：表示以u为父节点体积不大于j的最大价值
f[u][j-k]：由于此时要从son这个子树中取第k个物品（第k个物品就是体积为k，价值为f[son][k]的物品），所以f[u][j-k]表示从u父节点中取j-k个体积的最大价值
f[son][k]：表示从son这个子树中取k个体积的最大价值

代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=110;
int f[N][N];
int n,m;
int w[N];
int v[N];
int h[N];int ne[N];int e[N];int idx;
void add(int a,int b){
    ne[idx]=h[a];
    e[idx]=b;
    h[a]=idx++;
}
void dfs(int u){
    if(v[u]>m){
        return;
    }
    for(int i=h[u];i!=-1;i=ne[i]){//枚举物品组
        int son=e[i];
        dfs(son);
        for(int j=m-v[u];j>=0;j--){
            for(int k=0;k<=j;k++){
                f[u][j]=max(f[u][j],f[u][j-k]+f[son][k]);
            }
        }
    }
    //以上是算出了还没有算上u的最大价值，所以还要算一下加上u的价值
    for(int j=m;j>=0;j--){
        if(j>=v[u]){//如果能放入u的，就更新
            f[u][j]=f[u][j-v[u]]+w[u];
        }else{//不能的直接为0
            f[u][j]=0;
        }
    }
}
int main(){
    cin >> n >> m;
    int root;
    memset(h,-1,sizeof(h));
    for(int i=1;i<=n;i++){
        int c;
        cin >> v[i] >> w[i] >> c;
        add(c,i);
        if(c==-1)root=i;
    }
    dfs(root);
    cout << f[root][m];
}