题目描述

给你一个 m x n 的二进制矩阵 mat。

每一步，你可以选择一个单元格并将它反转（反转表示 0 变 1 ，1 变 0 ）。如果存在和它相邻的单元格，那么这些相邻的单元格也会被反转。（注：相邻的两个单元格共享同一条边。）

请你返回将矩阵 mat 转化为全零矩阵的 最少反转次数，如果无法转化为全零矩阵，请返回 -1。

二进制矩阵的每一个格子要么是 0 要么是 1 。

全零矩阵是所有格子都为 0 的矩阵。

样例

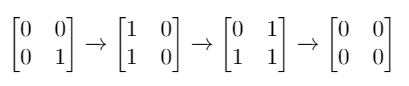
输入：mat = [[0,0],[0,1]]
输出：3
解释：一个可能的解是反转 (1, 0)，然后 (0, 1)，最后是 (1, 1)。

输入：mat = [[0]]
输出：0
解释：给出的矩阵是全零矩阵，所以你不需要改变它。

输入：mat = [[1,1,1],[1,0,1],[0,0,0]]
输出：6

输入：mat = [[1,0,0],[1,0,0]]
输出：-1
解释：该矩阵无法转变成全零矩阵。

限制

• m == mat.length
• n == mat[0].length
• 1 <= m <= 3
• 1 <= n <= 3
• mat[i][j] 是 0 或 1 。

算法1

(暴力枚举) $O(mn \cdot 2^{mn})$

1. 暴力枚举哪些位置需要反转，一共有 $2^{mn}$ 种方案。
2. 对于每种方案，验证最终是否为全 0。
3. 找到反转次数最少的方案。

时间复杂度

• 验证需要 $O(mn)$ 的时间复杂度，故总时间复杂度为 $O(mn \cdot 2^{mn})$。

空间复杂度

• 需要额外 $O(mn)$ 的空间，可以通过恢复现场来省略掉这部分空间。

C++ 代码

class Solution {
public:
    int minFlips(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();

        const int dx[5] = {0, 0, 1, 0, -1};
        const int dy[5] = {0, 1, 0, -1, 0};

        int ans = m * n + 1;

        for (int S = 0; S < (1 << m * n); S++) {
            int tot = 0;
            vector<vector<int>> tmp(m, vector<int>(n, 0));

            for (int i = 0; i < m * n; i++)
                if ((S >> i) & 1) {
                    tot++;
                    int x = i / n, y = i % n;

                    for (int j = 0; j < 5; j++) {
                        int tx = x + dx[j], ty = y + dy[j];
                        if (tx < 0 || tx >= m || ty < 0 || ty >= n)
                            continue;
                        tmp[tx][ty] ^= 1;
                    }
                }

            bool flag = true;
            for (int i = 0; i < m && flag; i++)
                for (int j = 0; j < n && flag; j++) {
                    if (tmp[i][j] ^ mat[i][j])
                        flag = false;
                }
            if (flag)
                ans = min(ans, tot);
        }
        if (ans == m * n + 1)
            ans = -1;

        return ans;
    }
};

算法2

(枚举第一行) $O(mn \cdot 2^n)$

1. 我们发现，如果确定了第一行（或第一列）反转哪些位置，则之后反转的位置就都可以确定。
2. 假设我们已经反转了第一行的某些位置，我们从第二行开始一直到最后一行，如果发现当前位置的上一行是 1，则当前位置需要进行反转。我们在之后每一行，都去填上一行留下的坑。
3. 最后判断下最后一行是否都已经变成了 0。

时间复杂度

• 仅需要枚举第一行的方案，然后进行整体的判断，故时间复杂度为 $O(mn \cdot 2^n)$。
• 如果列数较小，行数较大，则可以枚举第一列。

空间复杂度

• 需要额外 $O(mn)$ 的空间记录中间过程。

C++ 代码

class Solution {
public:
    int minFlips(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();

        const int dx[5] = {0, 0, 1, 0, -1};
        const int dy[5] = {0, 1, 0, -1, 0};

        int ans = m * n + 1;

        for (int S = 0; S < (1 << n); S++) {
            int tot = 0;
            vector<vector<int>> tmp(m, vector<int>(n, 0));

            for (int j = 0; j < n; j++)
                if ((S >> j) & 1) {
                    tot++;

                    for (int k = 0; k < 5; k++) {
                        int tx = 0 + dx[k], ty = j + dy[k];
                        if (tx < 0 || tx >= m || ty < 0 || ty >= n)
                            continue;
                        tmp[tx][ty] ^= 1;
                    }
                }

            for (int i = 1; i < m; i++)
                for (int j = 0; j < n; j++)
                    if (mat[i - 1][j] ^ tmp[i - 1][j]) {
                        tot++;

                        for (int k = 0; k < 5; k++) {
                            int tx = i + dx[k], ty = j + dy[k];
                            if (tx < 0 || tx >= m || ty < 0 || ty >= n)
                                continue;
                            tmp[tx][ty] ^= 1;
                        }
                    }

            bool flag = true;
            for (int j = 0; j < n; j++)
                if (mat[m - 1][j] ^ tmp[m - 1][j]) {
                    flag = false;
                    break;
                }

            if (flag)
                ans = min(ans, tot);
        }

        if (ans == m * n + 1)
            ans = -1;

        return ans;
    }
};