算法分析

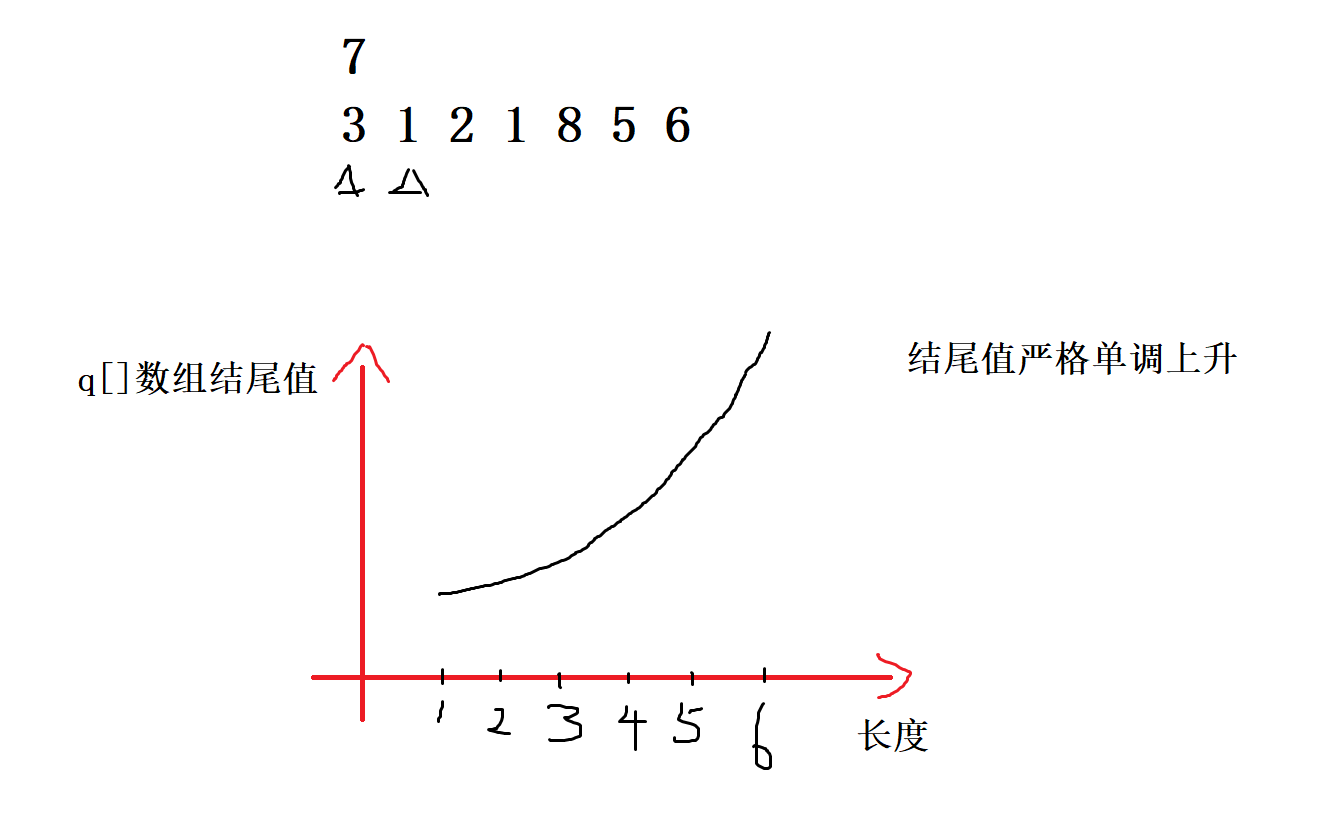
• 1、如图所示，在使用最长上升子序列 I 做法时，可以发现找到长度为1的上升子序列，若后面的数能接到3的后面，那么一定能接到1的后面，因为1比3更好，扩展度高

• 2、使用q[]存储所有不同长度的上升子序列结尾的最小值

• 3、进来一个数a[i]时，通过二分在q[]中找到最大的小于ai的数，就能够将ai接到该数的后面，即更新q[r + 1] = a[i]

扩展 最长上升子序列 求字典序问题

时间复杂度 $O(nlogn)$

参考文献

参考y总

Java 代码

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;

public class Main {
    static int N = 100010;
    static int n;
    static int[] a = new int[N];
    static int[] q = new int[N];
    public static void main(String[] args) throws NumberFormatException, IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(reader.readLine().trim());
        String[] s1 = reader.readLine().split(" ");
        for(int i = 0;i < n;i++) a[i] = Integer.parseInt(s1[i]);
        q[0] = Integer.MIN_VALUE;//可省略
        int len = 0;
        for(int i = 0;i < n;i++)
        {
            int l = 0,r = len;
            while(l < r)
            {
                int mid = (l + r + 1) >> 1;
                if(q[mid] < a[i]) l = mid;
                else r = mid - 1;

            }
            len = Math.max(len, r + 1);
            q[r + 1] = a[i];
        }
        System.out.println(len);
    }
}