多源汇最短路问题-具有多个源点
Floyd算法 O(n^3)-动态规划
给定一个n个点m条边的有向图,图中可能存在重边和自环,边权可能为负数。
再给定k个询问,每个询问包含两个整数x和y,表示查询从点x到点y的最短距离,如果路径不存在,则输出“impossible”。
数据保证图中不存在负权回路。
输入格式
第一行包含三个整数n,m,k
接下来m行,每行包含三个整数x,y,z,表示点x和点y之间存在一条有向边,边长为z。
接下来k行,每行包含两个整数x,y,表示询问点x到点y的最短距离。
输出格式
共k行,每行输出一个整数,表示询问的结果,若询问两点间不存在路径,则输出“impossible”。
数据范围
$1≤n≤200$
$1≤k≤n^2$
$1≤m≤20000$
图中涉及边长绝对值均不超过10000。
输入样例:
3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3
输出样例:
impossible
1
代码:
#include <iostream>
using namespace std;
const int N = 210, M = 2e+10, INF = 1e9;
int n, m, k, x, y, z;
int d[N][N];
void floyd() {
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
int main() {
cin >> n >> m >> k;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if(i == j) d[i][j] = 0;
else d[i][j] = INF;
while(m--) {
cin >> x >> y >> z;
d[x][y] = min(d[x][y], z);
//注意保存最小的边
}
floyd();
while(k--) {
cin >> x >> y;
if(d[x][y] > INF/2) puts("impossible");
//由于有负权边存在所以约大过INF/2也很合理
else cout << d[x][y] << endl;
}
return 0;
}
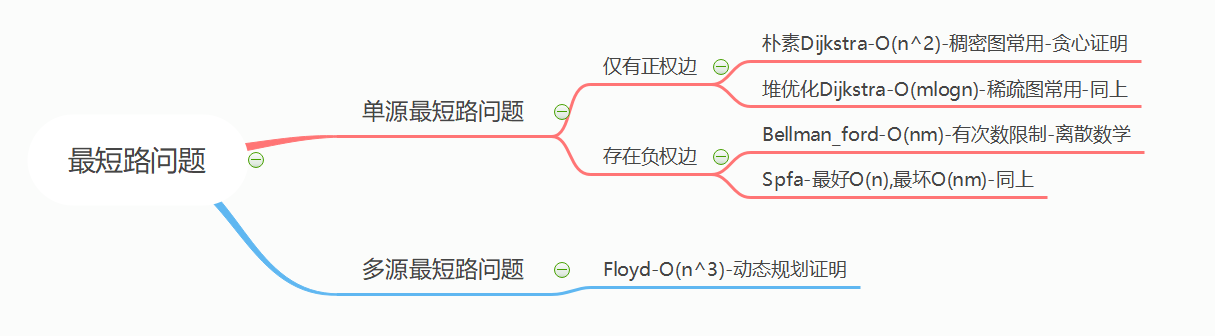
文字性复习
Dijkstra-朴素O(n^2)
- 初始化距离数组, dist[1] = 0, dist[i] = inf;
- for n次循环 每次循环确定一个min加入S集合中,n次之后就得出所有的最短距离
- 将不在S中dist_min的点->t
- t->S加入最短路集合
- 用t更新到其他点的距离
Dijkstra-堆优化O(mlogm)
- 利用邻接表,优先队列
- 在priority_queue[HTML_REMOVED], greater[HTML_REMOVED] > heap;中将返回堆顶
- 利用堆顶来更新其他点,并加入堆中类似宽搜
Bellman_fordO(nm)
- 注意连锁想象需要备份, struct Edge{inta,b,c} Edge[M];
- 初始化dist, 松弛dist[x.b] = min(dist[x.b], backup[x.a]+x.w);
- 松弛k次,每次访问m条边
Spfa O(n)~O(nm)
- 利用队列优化仅加入修改过的地方
- for k次
- for 所有边利用宽搜模型去优化bellman_ford算法
- 更新队列中当前点的所有出边
Floyd O(n^3)
- 初始化d
- k, i, j 去更新d


#### Dijkstra-朴素 $O(n^2)$
用t更新到其他点的距离
#### Dijkstra-堆优化 $O(mlogm)$
利用邻接表,优先队列
priority_queue<PII,vector<PII>,greater<PII>> heap;中将返回堆顶利用堆顶来更新其他点,并加入堆中类似宽搜
#### Bellman_ford $O(nm)$
注意连锁想象需要备份,
struct Edge{int a,b,c} Edge[M];dist[x.b] = min(dist[x.b], backup[x.a]+x.w);松弛k次,每次访问m条边
#### Spfa $O(n) \sim O(nm)$
利用队列优化仅加入修改过的地方
更新队列中当前点的所有出边
#### Floyd $O(n^3)$
初始化d
记录美好生活
你怎么敢记录的
你记录的怎么能是美好生活呢(bushi)
每天都记录美好生活啊你
https://www.acwing.com/activity/content/code/content/5667851/ 大家也可以看看这篇Floyd算法
大佬们,请问一下,在Floyd算法中初始化 边数组操作时 用的不是memset操作是为了保证i,j相等时值为0, 但在 dijkstra算法 和 prim算法 中用memset操作 直接初始化为正无穷 却可以,这是为什么呢
防止有其他数据影响最小集合的扩展,取正无穷可以避免加入到最小集中
dijkstra不处理自环不会影响结果吧,自环不会影响更新的结果,Floyd算法因为是用到了d[i]j这个状态来更新会影响结果
floyd中是有dis[i][i]但是dij不会而且dij的dis可以靠自己想怎么来怎么来
在dji对应的t点进行更新时,不会更新它自环的边,因为t点已经确定了是最短路里的一个点,遍历邻接点时就不会再经过t点,所以只要它自环的边权只要不是负的就都可以
SPFA算法的一般时间复杂度是O(m),是边的条数,最坏时间复杂度是O(n * m)
有人能解释一下,题目中的k次询问和y总说的经过1到k个中转点有什么关系吗?如果没有的话为什么不用不同的字母区分开?
有人可以解释一下,为什么DP的理解上,要引入第三维的k呀?在两维的理解上可以吗?我的理解是,二维的i,j相当于i,j对所有点(k)不断进行松弛操作,最后得到每一个edge的最短路径(如果存在的话),因此有g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
为什么 if(d[x][y] > INF/2) puts(“impossible”);
为什么是>=INF/2,而不是INF
老兄你明白了没,我还是看不懂为啥是inf/2,我觉得这只是个大概的估计,
比如呢 d[i][k] 是 INF 但是 d[k][j] 是 -2 巧了 更新的时候会不会更新它, 会吧, 但是是主动更新吗, 不是, 是被动更新, 因为 i是到不了k的, 所以k也是到不了j的, 那么i就到不了j, 你懂了吧
就比如1->2->3这条路径,如果1到2的距离是-2,2到3的距离是INF(说明2不能到3这个点),那么最终1到3的距离是INF-2,他不等于INF,但是1这个点到不了3这个点,所以当d[1][3]=INF-2(也就是>INF/2的时候)的时候,1是到不了3这个点的,所以输出impossible
因为有负权边,如果数据中足够多足够大的负权边,会把预设的0x3f3f3f3f更新地更小,但是又不会大于0x3f3f3f3f/2。因为,0x3f3f3f3f是略大于10^9的数,他的一半是510^8左右,比题目中限制的最大的2000010000也大得多,因此如果比这个一半要大的话就可以确定是由0x3f3f3f3f被负权边过来的,如果比它小的话,就肯定是存在最短路的。
floyd里动态规划的循环怎么看,k,i,j可以随便换层吗。
我按i,j,k的顺序发现WA了。
k一定要第一个,i,j的顺序可以变换
中转点要放在最外层
nb
感谢整理Orz
spfa写错了吧,一般不是o(m)?
说法不同
赞赞赞!
已点赞+收藏,感谢整理
你的文字很好,可惜下一秒就被我收藏了(doge)
hhh
666
666
大佬我可以问一下 这里d矩阵可以用0x3f存么
可以的,1e9和0x3f3f3f3f都是表示不可达
文字复习 特感
哈哈哈
收藏比点赞多就离谱
因为有的人懒得点赞
勤于收藏,懒得点赞 == 我爱白嫖
HTML_REMOVED这是啥
显示错误
666