LeetCode周赛题

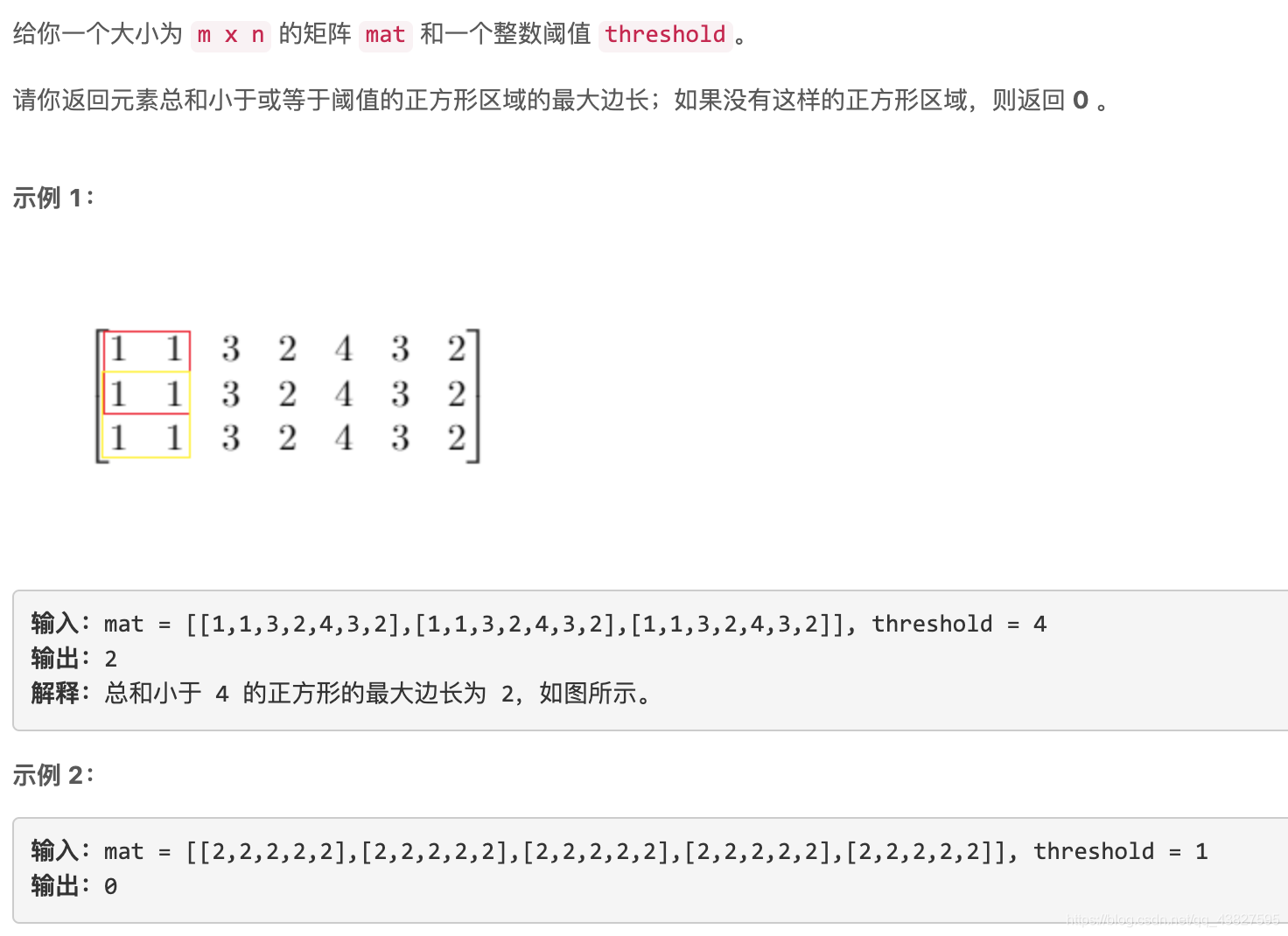
算法分析
前缀和+动态规划 时间复杂度:O(m * n * max(m, n)), 空间复杂度:O(n * m)
1. 这个题实际上是之前做过的最大边长的升级版
2. 需要额外计算一下前缀和，然后先求出可能的最长边长的上界，然后边长不断减减，直到不超过阈值
3. 最后更新f[i][j]和res即可

/**
 *    @Author: Wilson79
 *    @Datetime: 2019年12月15日 星期日 11:41:10
 *    @Filename: 元素和小于等于阈值的正方形的最大边长.cpp
 */


class Solution {
public:
    int maxSideLength(vector<vector<int>>& mat, int threshold) {
        int sum[310][310];
        memset(sum, 0, sizeof sum);
        int f[310][310];
        memset(f, 0, sizeof f);

        if (!mat.size() || !mat[0].size()) return 0;
        int m = mat.size(), n = mat[0].size();

        // 预处理前缀和
        for (int i = 1; i <= m; i ++) {
            for(int j = 1;  j <= n; j ++) {
                sum[i][j] = mat[i - 1][j - 1] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];
            }
        }

        int res = -1;
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j ++) {
                int t = min(f[i - 1][j - 1], min(f[i][j - 1], f[i - 1][j])) + 1;
                // 利用前缀和求子矩阵的和
                while(t > 0 && (sum[i][j] - sum[i - t][j] - sum[i][j - t] + sum[i - t][j - t] > threshold)) t --;
                f[i][j] = t;
                res = max(f[i][j], res);
            }
        }

        return res;
    }
};