题目描述
请你将一个16x16的数独填写完整,使得每行、每列、每个4x4十六宫格内字母A~P均恰好出现一次。
保证每个输入只有唯一解决方案。
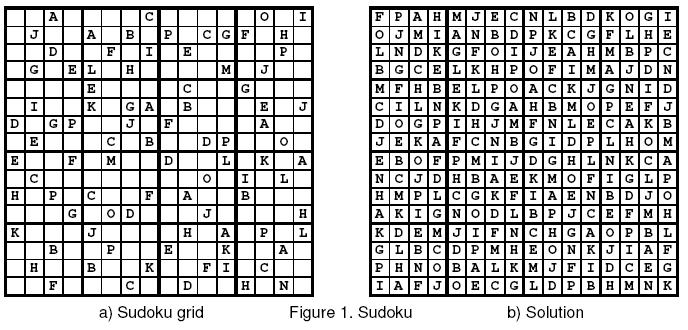
输入格式
输入包含多组测试用例。
每组测试用例包括16行,每行一组字符串,共16个字符串。
第i个字符串表示数独的第i行。
字符串包含字符可能为字母A~P或”-“(表示等待填充)。
测试用例之间用单个空行分隔,输入至文件结尾处终止。
输出格式
对于每个测试用例,均要求保持与输入相同的格式,将填充完成后的数独输出。
每个测试用例输出结束后,输出一个空行。
样例
输入样例:
--A----C-----O-I
-J--A-B-P-CGF-H-
--D--F-I-E----P-
-G-EL-H----M-J--
----E----C--G---
-I--K-GA-B---E-J
D-GP--J-F----A--
-E---C-B--DP--O-
E--F-M--D--L-K-A
-C--------O-I-L-
H-P-C--F-A--B---
---G-OD---J----H
K---J----H-A-P-L
--B--P--E--K--A-
-H--B--K--FI-C--
--F---C--D--H-N-
FPAHMJECNLBDKOGI
OJMIANBDPKCGFLHE
LNDKGFOIJEAHMBPC
BGCELKHPOFIMAJDN
MFHBELPOACKJGNID
CILNKDGAHBMOPEFJ
DOGPIHJMFNLECAKB
JEKAFCNBGIDPLHOM
EBOFPMIJDGHLNKCA
NCJDHBAEKMOFIGLP
HMPLCGKFIAENBDJO
AKIGNODLBPJCEFMH
KDEMJIFNCHGAOPBL
GLBCDPMHEONKJIAF
PHNOBALKMJFIDCEG
IAFJOECGLDPBHMNK
算法1
(暴搜+剪枝)
16×16数独是9×9数独的加强版,由于搜索范围增大继续使用原来的优化方案的话能T上天。
这里需要再原来的剪枝基础上增加新的剪枝手段。
首先, 每个空格,如果不能填则返回false;如果只有一个选项,则直接填上。
其实这个优化方案包含在原先的优化方案中,无非是少递归那么1.2层,加不加都无所谓。
其次,对于每一行,如果某个字母不能填,则返回false;如果某个字母只有一种填法,则直接填。
在经过第一种剪枝之后,对于每一行,虽然所有的空都有可选方案,但是字母A~P中可能会存在一些字母,不在该行中的所有可选方案以及已填字母中,显然这种情况一定是填的不对的情况,同时,也可能确定出某一字母一定只能填在某个空格中。
同理,对于每一列,每一区域都可以参照方案二的思路剪枝。
注意,在return false之前,一定要对现场的恢复。
C++ 代码
#include<bits/stdc++.h>
#define lowbit(x) ((x)&(-(x)))
using namespace std;
const int N = 16, M = N * N + 10;
int ones[1 << N], mp[1 << N];
char str[M], mem_str[M][M];
int row[N], col[N], cell[4][4], cnt, mem_row[M][N], mem_col[M][N], mem_cell[M][4][4];
inline void sheet() {
for (int i = 0; i < N; i++)
mp[1 << i] = i;
for (int i = 1; i < 1 << N; i++)
for (int j = i; j; j -= lowbit(j))
ones[i]++;
}
inline void init() {
for (int i = 0; i < N; i++)
row[i] = col[i] = (1 << N) - 1;
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
cell[i][j] = (1 << N) - 1;
}
inline void build() {
int k = 0;
cnt = 0;
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++, k++)
if (str[k] != '-') {
int t = str[k] - 'A';
row[i] -= 1 << t;
col[j] -= 1 << t;
cell[i / 4][j / 4] -= 1 << t;
} else cnt++;
}
inline int get(int x, int y) {
return row[x] & col[y] & cell[x / 4][y / 4];
}
inline void change(int x, int y, int c) {
row[x] -= c;
col[y] -= c;
cell[x / 4][y / 4] -= c;
str[x * 16 + y] = 'A' + mp[c];
}
inline void recove(int x, int y, int c) {
row[x] += c;
col[y] += c;
cell[x / 4][y / 4] += c;
str[x * 16 + y] = '-';
}
inline void back(int ktot) {
memcpy(str, mem_str[ktot], sizeof(str));
memcpy(row, mem_row[ktot], sizeof(row));
memcpy(col, mem_col[ktot], sizeof(col));
memcpy(cell, mem_cell[ktot], sizeof(cell));
}
bool dfs(int tot) {
if (tot == cnt)return true;
int ktot = tot;
memcpy(mem_str[ktot], str, sizeof(str));
memcpy(mem_row[ktot], row, sizeof(row));
memcpy(mem_col[ktot], col, sizeof(col));
memcpy(mem_cell[ktot], cell, sizeof(cell));
int k = 0;
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++, k++)
if (str[k] == '-') {
int tc = ones[get(i, j)];
if (!tc) {
back(ktot);
return false;
} else if (tc == 1) {
change(i, j, get(i, j));
tot++;
}
}
for (int i = 0; i < N; i++) {
int sor = 0, sand = (1 << N) - 1;
for (int j = 0; j < N; j++) {
if (str[i * 16 + j] != '-') {
sor |= 1 << (str[i * 16 + j] - 'A');
continue;
}
int s = get(i, j);
sand &= ~(sor & s);
sor |= s;
}
if (sor != (1 << N) - 1) {
back(ktot);
return false;
}
for (int j = sand; j; j -= lowbit(j)) {
int t = lowbit(j);
for (k = 0; k < N; k++)
if ((str[i * 16 + k] == '-') && (row[i] & col[k] & cell[i / 4][k / 4] & t)) {
change(i, k, t);
tot++;
break;
}
}
}
for (int j = 0; j < N; j++) {
int sor = 0, sand = (1 << N) - 1;
for (int i = 0; i < N; i++) {
if (str[i * 16 + j] != '-') {
sor |= 1 << (str[i * 16 + j] - 'A');
continue;
}
int s = get(i, j);
sand &= ~(sor & s);
sor |= s;
}
if (sor != (1 << N) - 1) {
back(ktot);
return false;
}
for (int i = sand; i; i -= lowbit(i)) {
int t = lowbit(i);
for (k = 0; k < N; k++)
if ((str[k * 16 + j] == '-') && (row[k] & col[j] & cell[k / 4][j / 4] & t)) {
change(k, j, t);
tot++;
break;
}
}
}
for (int ci = 0; ci < 4; ci++)
for (int cj = 0; cj < 4; cj++) {
int sor = 0, sand = (1 << N) - 1;
for (int i = ci * 4; i < ci * 4 + 4; i++)
for (int j = cj * 4; j < cj * 4 + 4; j++) {
if (str[i * 16 + j] != '-') {
sor |= 1 << (str[i * 16 + j] - 'A');
continue;
}
int s = get(i, j);
sand &= ~(sor & s);
sor |= s;
}
if (sor != (1 << N) - 1) {
back(ktot);
return false;
}
for (k = sand; k; k -= lowbit(k)) {
int t = lowbit(k);
for (int i = ci * 4; i < ci * 4 + 4; i++)
for (int j = cj * 4; j < cj * 4 + 4; j++)
if ((str[i * 16 + j] == '-') && (row[i] & col[j] & cell[i / 4][j / 4] & t)) {
change(i, j, t);
tot++;
break;
}
}
}
if (tot == cnt)return true;
int mn = 17, x, y;
k = 0;
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++, k++)
if (str[k] == '-' && ones[get(i, j)] < mn)
x = i, y = j, mn = ones[get(i, j)];
for (int i = get(x, y); i; i -= lowbit(i)) {
int t = lowbit(i);
change(x, y, t);
if (dfs(tot + 1))return true;
recove(x, y, t);
}
back(ktot);
return false;
}
void solve() {
dfs(0);
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++)cout << str[i * 16 + j];
cout << endl;
}
cout << endl;
}
int main() {
sheet();
while (cin >> str[0]) {
for (int i = 1; i < N * N; i++)cin >> str[i];
init();
build();
solve();
}
return 0;
}

