算法分析

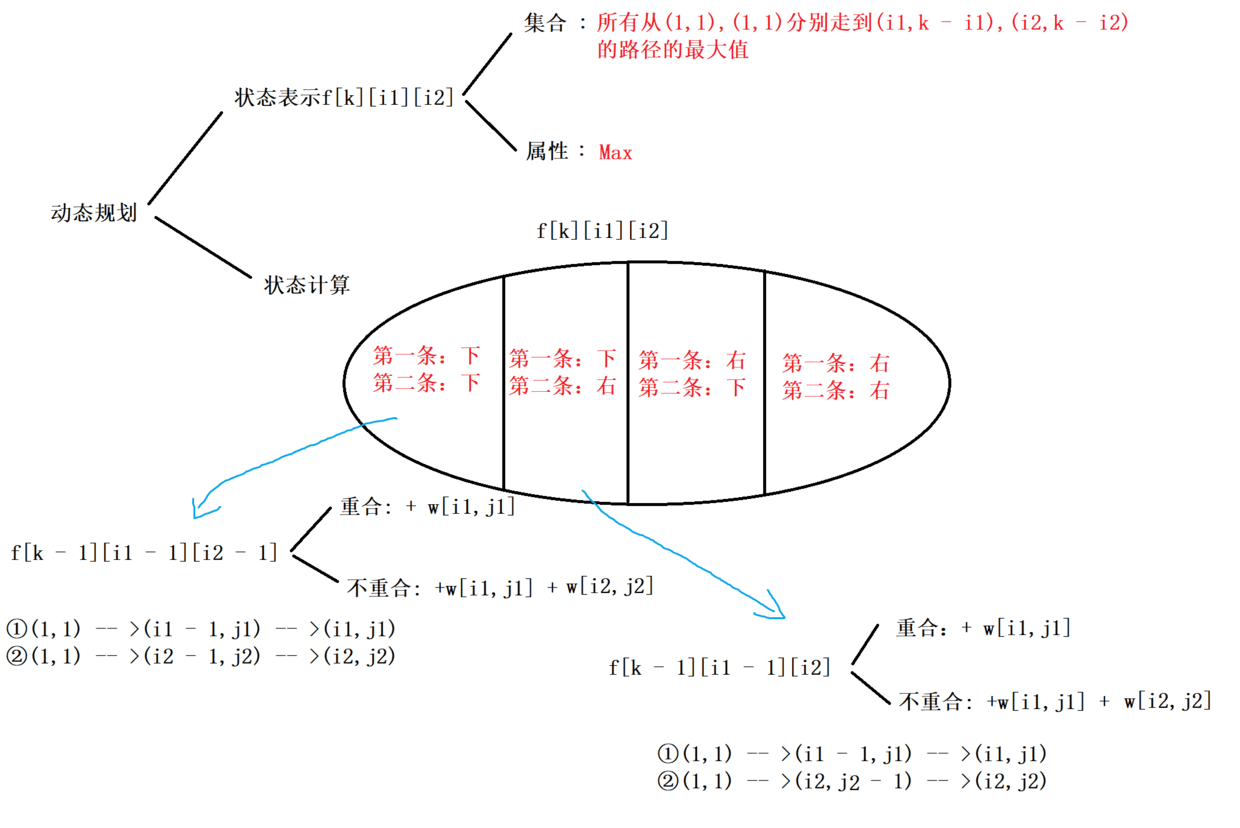
• 1、f[i1,j1,i2,j2]表示所有从(1,1),(1,1)分别走到(i1,j1),(i2,j2)的路径的最大值

• 2、由于走两次可以看成是两条路径同时走，因此k表示两条路线当前走到的各自的横纵坐标之和k == i1 + j1 == i2 + j2

注意：只有在i1 + j1 == i2 + j2时，两条路径走到的当前格子才可能重合

时间复杂度 $O(n^3)$

参考文献

算法提高课

Java 代码

import java.util.Scanner;

public class Main {
    static int N = 15;
    static int[][][] f = new int[N * 2][N][N];
    static int[][] w = new int[N][N];
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        while(true)
        {
            int a = scan.nextInt();
            int b = scan.nextInt();
            int c = scan.nextInt();
            if(a == 0 || b == 0 || c == 0) break;
            w[a][b] = c;
        }

        for(int k = 2;k <= n * 2;k ++)
            for(int i1 = 1;i1 <= n;i1 ++)
                for(int i2 = 1;i2 <= n;i2 ++)
                {
                    int j1 = k - i1;
                    int j2 = k - i2;
                    if(j1 <= 0 || j1 > n || j2 <= 0 || j2 > n) continue;

                    int t = w[i1][j1];
                    if(i1 != i2) t += w[i2][j2];//若路径重合
                    int x = f[k][i1][i2];
                    x = Math.max(x, f[k - 1][i1 - 1][i2 - 1] + t);
                    x = Math.max(x, f[k - 1][i1 - 1][i2] + t);
                    x = Math.max(x, f[k - 1][i1][i2 - 1] + t);
                    x = Math.max(x, f[k - 1][i1][i2] + t);
                    f[k][i1][i2] = x;
                }
        System.out.println(f[n * 2][n][n]);
    }
}