凭啥秦淮岸他代码就那么短…

好吧,我们来分析这个题.每个点都恰有一条出边,所以一个基环树森林.

假设询问的点是$u,v$

• 如果$u,v$不在同一颗基环树中,就是-1 -1.我用了一个叫block的并查集来维护联通性,很简单.

所以我们接下来考虑$u,v$联通的情况.环上的每个点连接的不在环上的部分一定形成一棵树,不妨把它叫做这个点的子树
每个父亲向儿子连边,就可以建出这些子树.我们还可以顺便用叫root的并查集来维护子树的根.

• 如果$u,v$在同一棵子树中,那么让它们走到LCA处显然是最优的,树剖LCA求一下就好了.

而如果$u,v$的根是两个不同的点呢?
举个例子(蓝色的就是环):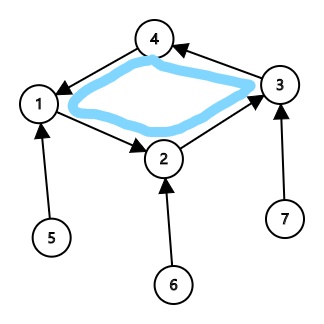

如果$u=5,v=6$
首先,它们肯定要先跳到各自的根那里,也就是$u=1,v=2$
我们有两种选择:让1走到2,或者让2走到1.前者$x=2,y=1$后者$x=1,y=3$
题目要求$max(x,y)$最小,所以前者更优.
更一般地,设$u,v$跳到各自的根上的代价分别是$x,y$,并且$x$走到$y$的代价是$cost_x$,$y$走到$x$的代价是$cost_y$
那么这种情况就表示为:

• 如果$x+cost_x<y+cosy_y$,就让$u$走到$v$.
• 如果$x+cost_x>y+cost_y$,就让$v$走到$u$

但我们还漏掉了$x+cost_x=y+cost_y$的情况(这个时候无论怎么走,$max(x,y)$都已经最小了).后面还有两个限制条件:$min(x,y)$最小,$x\ge y$
类似于$u=5,v=7$的情况.如果让$u$走到$u$,结果是$x=3,y=1$,让$v$走到$u$结果是$x=1,y=3$.所以选择前者.
这种情况表示为:

• 如果$x+cost_x=y+cosy_y$,并且$x\ge y$,就让$u$走到$v$
• 如果$x+cost_x=y+cosy_y$,并且$x< y$,就让$v$走到$u$

读者可以再根据上面的图理解一下.
哦还有,就是$cost_x$和$cost_y$的求法,读者可以先dfs求出每个环的大小,和每个点被访问到的时间戳,差值就是距离(可见代码)

预处理$O(n)$,每次询问至多$O(logn)$,总时间复杂度$O(nlogn)$
代码有点长??不过为了可读性,我有很多空行,将代码分段(有一些注释)

/**********/省略快读
#define MAXN 500011
struct Union_Find_Set//封装的并查集
{
    ll fa[MAXN];
    void build(ll n)
    {
        for(ll i=1;i<=n;++i)fa[i]=i;
    }
    ll find(ll x)
    {
        if(fa[x]==x)return x;
        return fa[x]=find(fa[x]);
    }
    void uni(ll u,ll v)
    {
        u=find(u),v=find(v);
        fa[u]=v;
    }
    bool same(ll u,ll v)
    {
        return find(u)==find(v);
    }
}block,root;//维护联通块的并查集,维护子树根的并查集
ll to[MAXN];//原图中的边
struct Edge//子树的边
{
    ll v,nxt;
}e[MAXN<<1|1];
ll cnt=0,last[MAXN];
void adde(ll u,ll v)//子树上加边
{
    ++cnt;
    e[cnt].v=v;
    e[cnt].nxt=last[u],last[u]=cnt;
}

ll fa[MAXN],dep[MAXN],size[MAXN],mson[MAXN];//树剖LCA部分,都是板子
void dfs1(ll u,ll now)
{
    dep[u]=now;
    size[u]=1;
    for(ll i=last[u];i;i=e[i].nxt)
    {
        ll v=e[i].v;
        if(dep[v])continue;
        fa[v]=u;
        dfs1(v,now+1);
        size[u]+=size[v];
        if(size[v]>size[mson[u]])mson[u]=v;
    }
}
ll top[MAXN],t[MAXN],tot=0;
void dfs2(ll u,ll cur)
{
    top[u]=cur;t[u]=++tot;
    if(mson[u])dfs2(mson[u],cur);
    for(ll i=last[u];i;i=e[i].nxt)
    {
        ll v=e[i].v;
        if(v==fa[u]||v==mson[u])continue;
        dfs2(v,v);
    }
}
ll LCA(ll u,ll v)
{
    while(top[u]!=top[v])
    {
        if(dep[top[u]]>=dep[top[v]])u=fa[top[u]];
        else v=fa[top[v]];
    }
    if(dep[u]>=dep[v])return v;
    else return u;
}

ll num[MAXN],len[MAXN],dfn[MAXN],cur=0;//点是被哪一次dfs访问到的,环的长度,时间戳,进行了几次dfs
bool loop[MAXN];//是否在环上
void find_loop(ll u)//dfs求环
{
    num[u]=++cur;
    ll tmp=to[u];
    while(!num[tmp])//找到第一个被访问过的点
    {
        num[tmp]=cur;
        tmp=to[tmp];
    }
    if(num[tmp]==cur)//是这一次被访问到,那么就构成了一个环,求一下环长并标记
    {
        ll t=0;
        len[cur]=1;
        loop[tmp]=1;dfn[tmp]=++t;
        ll pos=to[tmp];
        while(pos!=tmp)
        {
            ++len[cur];
            loop[pos]=1;dfn[pos]=++t;
            pos=to[pos];
        }
    }
    //否则之前已经访问过了,就不再处理
}

int main()
{
    ll n=read(),q=read();
    block.build(n),root.build(n);
    for(ll i=1;i<=n;++i)
    {
        to[i]=read();
        block.uni(i,to[i]);//联通块维护
    }

    for(ll i=1;i<=n;++i)//注意图不一定联通
        if(!num[i])find_loop(i);
    for(ll i=1;i<=n;++i)
        if(!loop[i])//当前点不在环上就是在子树上,加边
        {
            root.uni(i,to[i]);//维护子树根
            adde(to[i],i);
        }
    for(ll i=1;i<=n;++i)//树剖预处理
        if(loop[i])dfs1(i,1),dfs2(i,i);

    for(ll i=1;i<=q;++i)
    {
        ll u=read(),v=read();
        if(!block.same(u,v))//不在一个连通块中的情况
        {
            puts("-1 -1");
            continue;
        }
        if(root.same(u,v))//在同一颗子树中
        {
            ll lca=LCA(u,v);
            printf("%lld %lld\n",dep[u]-dep[lca],dep[v]-dep[lca]);
            continue;
        }
        //剩下的就是在环上的情况
        ll x=dep[u]-1,y=dep[v]-1,cost_x,cost_y;
        u=root.find(u),v=root.find(v);
        if(dfn[u]<=dfn[v])cost_x=dfn[v]-dfn[u],cost_y=len[num[u]]-cost_x;//时间戳相减求cost_x和cost_y
        else cost_y=dfn[u]-dfn[v],cost_x=len[num[u]]-cost_y;

        if(x+cost_x<y+cost_y||(x+cost_x==y+cost_y&&x>=y))printf("%lld %lld\n",x+cost_x,y);
        else printf("%lld %lld\n",x,y+cost_y);
    }
    return 0;
}