博客园食用通道 (出于某种技术原因,ACwing的图片可能会崩,最好前往博客园阅读 =^-^=)
Problem
Solution
好题,代码短,思维性强,细节多。
我们应该推导出以下两条性质:
-
让我们来手玩一下样例,样例排序后应该是这样子的:
0 3 3 6 6 9,其中相同的数在排序后的序列是连续的一段,而双端队列中元素应该是序列中连续的一段。(并没有用) -
双端队列添加元素,先是添加一个到中间,再是往两边插入数字,假设双端队列中一段元素分别是 $x_1,x_2…x_n$ ,且 $x_m$ 是第一个加入的元素。记 $ID(x_i)$ 表示这个元素在原序列中的下标,那么就有 $ID(x_1)>ID(x_2)>…>ID(x_{m-1})>ID(x_m)<ID(x_{m+1})<…<ID(x_{n-1})<ID(x_n)$。(这个性质就很重要了)
考虑一个双端队列,用函数 $y=ID(x_i)$ 来形象的表示这个数列的特征(当然这个函数是离散的,为了形象,将他连续),函数的图像如下:
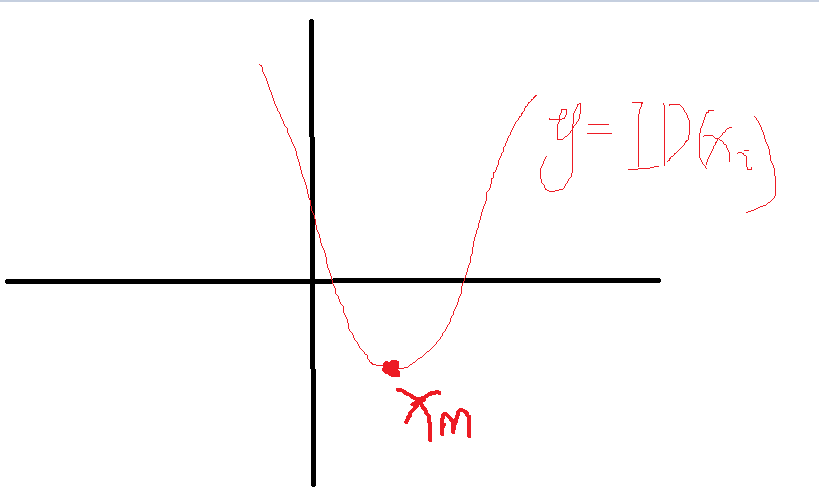
它是一个单谷函数!
我们把原序列排好序,它们的下标排成一个函数(相同的数字下标直接按从小到大排,先不做处理),函数的图像应该是这样子的:
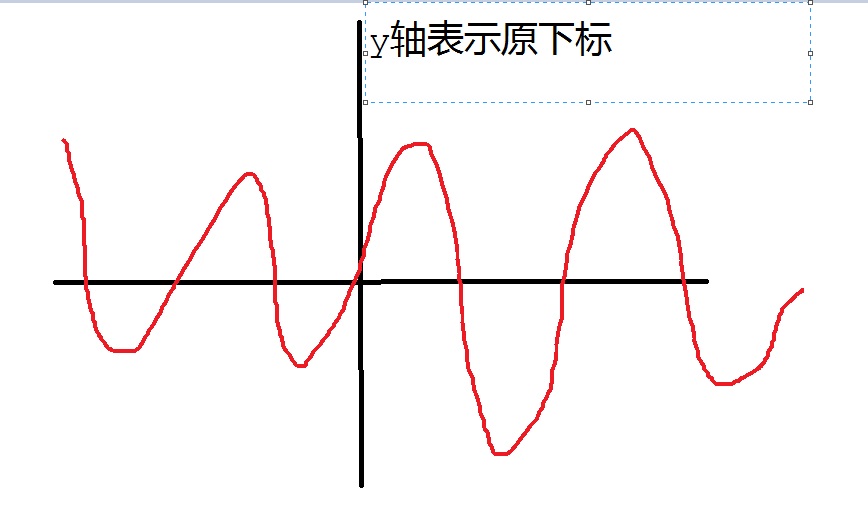
波浪形的。又因为双端队列中的元素必须是原序列中连续的一段,所以我们就把问题转化为在上面这个函数里面找谷底,一个谷底就是一个双端队列 (懂?)
诶诶诶,别走啊,这个题目还没做完呢,我们还不能保证这样是最优的(也就是波谷是最少的),我们要用一些贪心策略来使得波谷最少。
这就要请出连在一起(值相同)的这些数了。我们知道,连在一起(值相同)的这些数内部都是这个样子的:
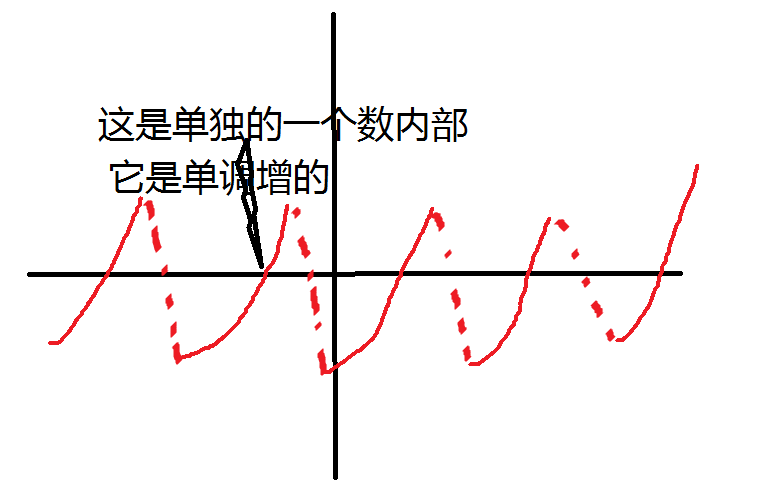
我们要用一些操作把这个函数尽量捋平,又因为我们发现值相同的这些数内部不是单调增就是单调减的(因为这样才会优),大力分类讨论,看一下哪一种会使得这个函数更加平整(上升趋势就尽量往上升,下降趋势就尽量往下降)。
最后注意一个细节,我们不是数有多少个波谷,而是数有多少个波峰,因为:
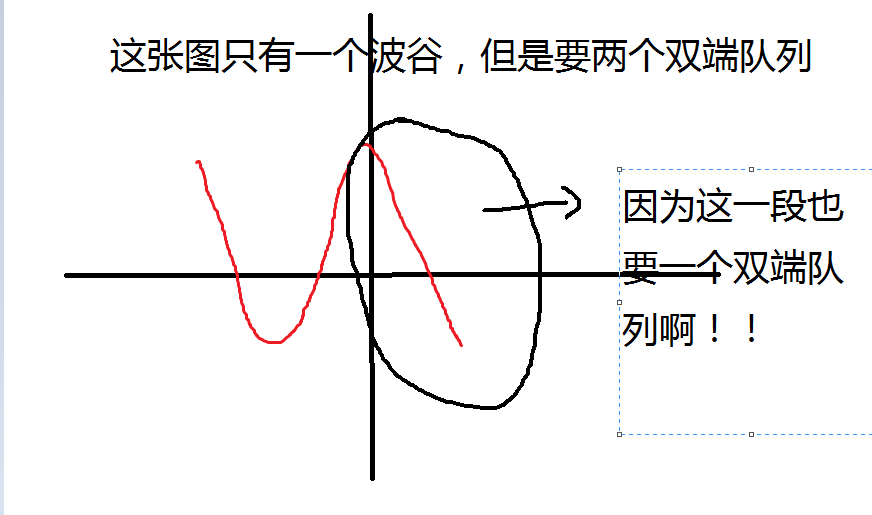
(自己多写写,多画画,结合这篇题解和代码思考思考,我觉得还是可以搞懂这题的)
Code
Talk is cheap.Show me the code.
#include<bits/stdc++.h>
#define INF 1e18
#define int long long
using namespace std;
inline int read() {
int x=0,f=1; char ch=getchar();
while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
return x * f;
}
const int N = 200007;
int n,ans;
struct Node {
int val,id;
bool operator < (const Node &el) {
if(val == el.val) return id < el.id;
return val < el.val;
}
}a[N];
signed main()
{
n = read();
for(int i=1,x;i<=n;++i) {
x = read();
a[i] = (Node)<%x,i%>;
}
sort(a+1, a+1+n);
int last = INF, dir = -1; ans = 1;
for(int i=1,j;i<=n;i=j+1) {
j = i; while(j<=n && a[i].val==a[j].val) ++j; --j;
int mip = a[i].id, mxp = a[j].id;
if(dir == 1) {
if(mip > last) last = mxp;
else last = mip, dir = -1, ++ans; //开启一个新的谷
} else {
if(mxp < last) last = mip;
else last = mxp, dir = 1;
}
}
printf("%lld\n",ans);
return 0;
}
Summary
这是一道思维题,但是还是可以学到套路的,学到了:
-
如果按顺序依次将数插入双端队列,那么双端队列具有一个性质,它里面的数的下标呈一个单谷函数
-
贪心使得函数波折尽量小的套路 (虽然这个自己想想就知道)

