题目描述

给你一个大小为 m x n 的矩阵 mat 和一个整数阈值 threshold。

请你返回元素总和小于或等于阈值的正方形区域的最大边长；如果没有这样的正方形区域，则返回 0。

样例

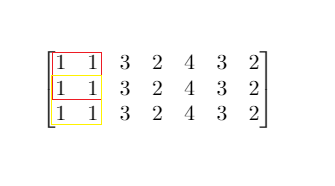
输入：mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
输出：2
解释：总和小于 4 的正方形的最大边长为 2，如图所示。
示例 2：

输入：mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
输出：0
示例 3：

输入：mat = [[1,1,1,1],[1,0,0,0],[1,0,0,0],[1,0,0,0]], threshold = 6
输出：3
示例 4：

输入：mat = [[18,70],[61,1],[25,85],[14,40],[11,96],[97,96],[63,45]], threshold = 40184
输出：2

限制

• 1 <= m, n <= 300
• m == mat.length
• n == mat[i].length
• 0 <= mat[i][j] <= 10000
• 0 <= threshold <= 10^5

算法

(前缀和 + 暴力枚举) $O(mn \min(m,n))$

1. 求出前缀矩形数组 sum。
2. 枚举正方形的边长，然后枚举每个正方形，如果求出的正方形内部的和小于等于 threshold，则返回边长。

时间复杂度

• 求前缀和的时间复杂度为 $O(mn)$。
• 边长共有 $\min(m, n)$ 种，每种都需要 $O(mn)$ 的时间。
• 故总时间复杂度为 $O(mn \min(m,n))$。

空间复杂度

• 需要额外 $O(mn)$ 的空间存储前缀和。

C++ 代码

class Solution {
public:
    int maxSideLength(vector<vector<int>>& mat, int threshold) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> sum(m + 1, vector<int>(n + 1, 0));
        for (int i = 1; i <= m; i++)
            for (int j = 1; j <= n; j++)
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1];

        for (int s = min(m, n); s >= 1; s--)
            for (int i = 1; i <= m - s + 1; i++)
                for (int j = 1; j <= n - s + 1; j++) {
                    int x = i + s - 1, y = j + s - 1;
                    if (sum[x][y] - sum[i - 1][y] - sum[x][j - 1] + sum[i - 1][j - 1] <= threshold)
                        return s;
                }

        return 0;
    }
};

算法2

(前缀和 + 二分) $O(mn \log \min(m, n)))$

1. 将算法 1 中对边长的暴力枚举改为二分枚举，可以节省大量的时间。

时间复杂度

• 仅需要判断 $O(\log \min(m, n))$ 次，故时间复杂度为 $O(mn \log \min(m, n)))$。

空间复杂度

• 需要额外 $O(mn)$ 的空间存储前缀和。

C++ 代码

class Solution {
public:
    bool check(int s, const vector<vector<int>>& sum, int m, int n, int threshold) {
        for (int i = 1; i <= m - s + 1; i++)
            for (int j = 1; j <= n - s + 1; j++) {
                int x = i + s - 1, y = j + s - 1;
                if (sum[x][y] - sum[i - 1][y] - sum[x][j - 1] + sum[i - 1][j - 1] <= threshold)
                    return true;
            }
        return false;
    }

    int maxSideLength(vector<vector<int>>& mat, int threshold) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> sum(m + 1, vector<int>(n + 1, 0));
        for (int i = 1; i <= m; i++)
            for (int j = 1; j <= n; j++)
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1];

        int l = 1, r = min(m, n);
        while (l < r) {
            int mid = (l + r) >> 1;
            if (check(mid + 1, sum, m, n, threshold))
                l = mid + 1;
            else
                r = mid;
        }

        if (check(l, sum, m, n, threshold))
            return l;

        return 0;
    }
};

算法3

(前缀和 + 双指针) $O(mn)$

1. 对于非负整数的一维数组中，求最长不超过 threshold 的子数组，可以采用双指针的解法在线性时间内求解。简单描述下，就是对于每个固定的右端点，其最小的合法左端点总是单调不减的。
2. 二维数组同理，我们把一个对角线上的位置看做一个一维数组，一共有 $m + n$ 个对角线，利用一维数组的思路，可以完成求解。

时间复杂度

• 每个对角线的每个位置最多遍历两次，故时间复杂度为 $O(mn)$。

空间复杂度

• 需要额外 $O(mn)$ 的空间存储前缀和。

C++ 代码

class Solution {
public:
    int getsum(int x1, int y1, int x2, int y2, const vector<vector<int>>& sum) {
        return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
    }

    int maxSideLength(vector<vector<int>>& mat, int threshold) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> sum(m + 1, vector<int>(n + 1, 0));
        for (int i = 1; i <= m; i++)
            for (int j = 1; j <= n; j++)
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1];

        int ans = 0;

        for (int s = 1 - n; s <= m - 1; s++) {
            int l = max(1, 1 + s);
            for (int i = l; i <= m && i - s <= n; i++) {
                while (getsum(l, l - s, i, i - s, sum) > threshold)
                    l++;
                ans = max(ans, i - l + 1);
            }
        }

        return ans;
    }
};