很久以前就见过这个题,今天算是过掉了.

结论:$(x,y)$到$(n,m)$的路径数量是$C^{n-x}_{n-x+m-y}$
写个$O(hw)$的暴力dp就能推得了,但此题$h,w$却在$10^5$级别…
不过$n$比较小,考虑对$n$进行dp.

用容斥:$(1,1)$到$(x,y)$的合法路径数=$(1,1)$到$(x,y)$的总路径数$-(1,1)$到$(x,y)$的经过禁点的路径数.
前面的部分就是$C^{x-1}_{x-1+y-1}$,预处理阶乘和逆元求一下就好了.
后者略麻烦些.
考虑经过一个禁点后后面任意的路径都属于经过禁点的路径,并且一个禁点$(vx,vy)$对$(x,y)$会有贡献当且仅当$vx\le x,vy\le y$,那么这个$(vx,vy)$就会产生$C^{x-vx}_{x-vx+y-vy}$条经过禁点的路径,把它减掉.
具体地说,先把所有禁点以$x$为第一关键字,$y$为第二关键字排序,消除后效性.
设f[i]表示到禁点i的合法路径数量(不妨设第$n+1$个禁点是$(h,w)$,这样$f[n+1]$就是最终答案)

那么$$f[i]=C^{x-1}_{x-1+y-1}-\sum_{j=0}^{i-1}f[j]*C^{x-vx}_{x-vx+y-vy}\ (vx\le x,vy\le y)$$

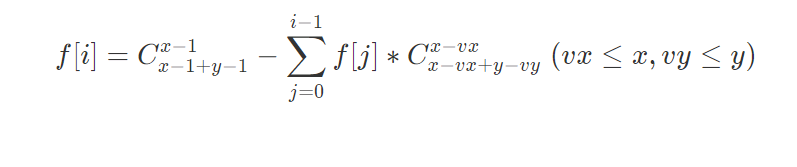
(可能latex坏了,我贴个图片)
时间复杂度显然$O(n^2)$,不过还有预处理逆元的$O(ElogE)$

附:隐隐感觉可以$O(nlogn+ElogE)$做,我再想想.
Code:

/**********/省略快读
#define MAXE 200011
#define MAXN 2011
ll fac[MAXE],inv[MAXE];
const ll mod=ll(1e9+7);
ll Qpow(ll a,ll p)
{
    ll res=1;
    while(p)
    {
        if(p&1)res=(res*a)%mod;
        a=(a*a)%mod;
        p>>=1;
    }
    return res;
}
ll C(ll n,ll m)//组合数
{
    return fac[n]*inv[m]%mod*inv[n-m]%mod;
}

pll a[MAXN];//禁点坐标
ll f[MAXN];
int main()
{
    ll h=read(),w=read();
    fac[0]=1,inv[0]=1;
    for(ll i=1;i<MAXE;++i)//预处理阶乘&组合数
    {
        fac[i]=fac[i-1]*i%mod;
        inv[i]=Qpow(fac[i],mod-2);
    }
    ll n=read();
    for(ll i=1;i<=n;++i)a[i].first=read(),a[i].second=read();
    a[n+1]=pll(h,w);
    std::sort(a+1,a+n+2);//排序消除后效性
    for(ll i=1;i<=n+1;++i)
    {
        ll x=a[i].first,y=a[i].second;
        f[i]=C(x-1+y-1,x-1);//总方案数
        for(ll j=1;j<i;++j)
        {
            ll vx=a[j].first,vy=a[j].second;
            if(vx<=x&&vy<=y)f[i]=(f[i]-f[j]*C(x-vx+y-vy,x-vx)%mod)%mod;//按照式子减去不合法的
        }
    }
    printf("%lld",(f[n+1]+mod)%mod);
    return 0;
}