题目描述
给你一个正方形字符数组 board ,你从数组最右下方的字符 ‘S’ 出发。
你的目标是到达数组最左上角的字符 ‘E’ ,数组剩余的部分为数字字符 1, 2, …, 9 或者障碍 ‘X’。在每一步移动中,你可以向上、向左或者左上方移动,可以移动的前提是到达的格子没有障碍。
一条路径的 「得分」 定义为:路径上所有数字的和。
请你返回一个列表,包含两个整数:第一个整数是 「得分」 的最大值,第二个整数是得到最大得分的方案数,请把结果对 10^9 + 7 取余。
如果没有任何路径可以到达终点,请返回 [0, 0] 。
样例
示例 1:
输入:board = ["E23","2X2","12S"]
输出:[7,1]
示例 2:
输入:board = ["E12","1X1","21S"]
输出:[4,2]
示例 3:
输入:board = ["E11","XXX","11S"]
输出:[0,0]
提示:
2 <= board.length == board[i].length <= 100
算法1
解答
使用动态规划 因为走到当前的格子肯定是当前格子的右方 下方和右下方。 那么他的右下方 右方和下方的状态中 那些是得分最高的就决定了当前的得分和走法方案数
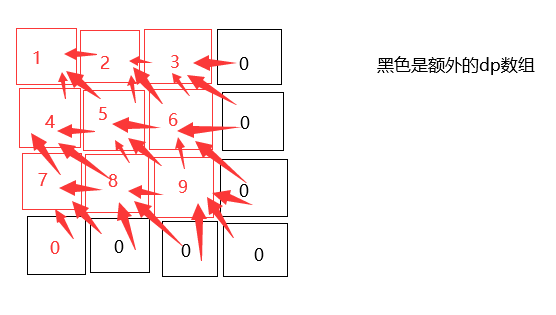
代码如下 注意DP有额外多开一层 为了保持代码的一致性。
代码起点dp判断如下: n = board.size() ; dp[n-1][n-1] = max(max(dp[n][n-1], dp[n-1][n]), dp[n][n]);
由于dp初始均为0 所以不影响起点 dp[n-1][n-1]的取值
C++ 代码
class Solution {
public:
vector<vector<int>> dp;
vector<vector<int>> path;
vector<int> pathsWithMaxScore(vector<string>& board) {
const int n = board.size();
const int MOD = 1e9+7;
dp.resize(n+1, vector<int>(n+1));
path.resize(n+1,vector<int>(n+1));
board[n - 1][n - 1] = '0';
board[0][0] = '0';
path[n - 1][n - 1] = 1;
for (int i = n - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
if (board[i][j] == 'X') continue;
int m = max(max(dp[i + 1][j], dp[i][j + 1]), dp[i + 1][j + 1]);
dp[i][j] = ( (board[i][j] - '0') + m ) %MOD;
if (dp[i + 1][j] == m) path[i][j] = ( path[i][j]+path[i+1][j])%MOD;
if (dp[i + 1][j+1] == m) path[i][j] = (path[i][j] + path[i + 1][j+1]) %MOD ;
if (dp[i][j+1] == m) path[i][j] = ( path[i][j]+ path[i][j+1])%MOD;
}
}
if(path[0][0] == 0) return vector<int>({0,0});
return vector<int>({dp[0][0],path[0][0]});
}
};

