题目描述

在一个二维的花园中，有一些用 (x, y) 坐标表示的树。由于安装费用十分昂贵，你的任务先用最短的绳子围起所有的树。

只有当所有的树都被绳子包围时，花园才能围好栅栏。

你需要找到正好位于栅栏边界上的树的坐标。

样例

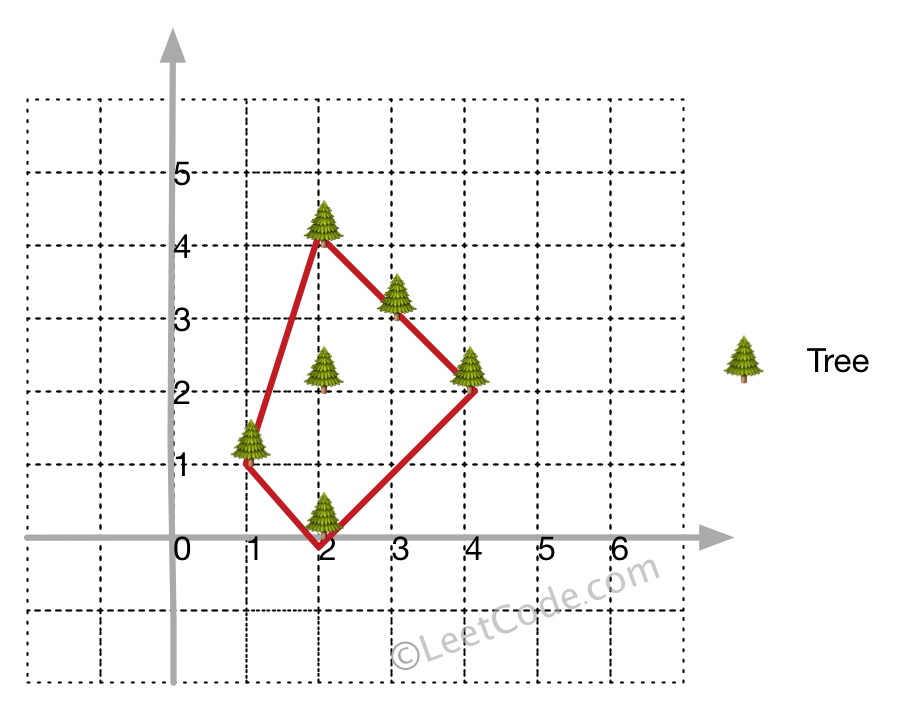
输入：[[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
输出：[[1,1],[2,0],[4,2],[3,3],[2,4]]

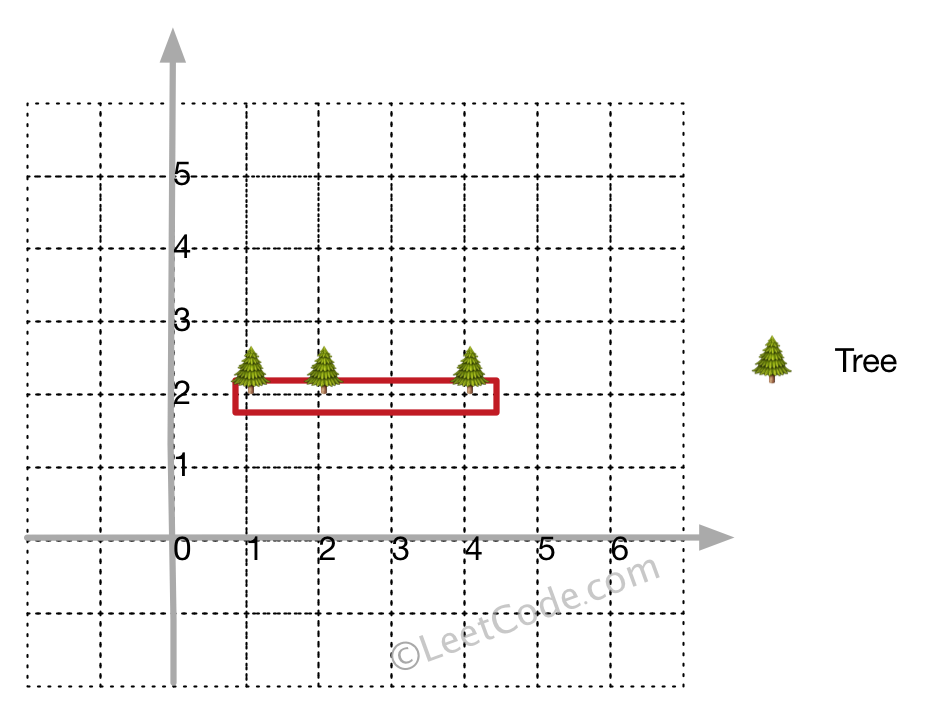
输入：[[1,2],[2,2],[4,2]]
输出：[[1,2],[2,2],[4,2]]
解释：即使树都在一条直线上，你也需要先用绳子包围它们。

提示

• 所有的树应当被围在一起。你不能剪断绳子来包围树或者把树分成一组以上。
• 输入的整数在 0 到 100 之间。
• 花园至少有一棵树。
• 所有树的坐标都是不同的。
• 输入的点没有顺序。输出顺序也没有要求。

算法

(凸包，栈) $O(n \log n)$

1. 不妨现将所有的点按横坐标从小到大排序。
2. 整个求凸包的过程分为两个阶段，第一个阶段先求下方和右方的凸包点，第二个阶段求上方和左方的凸包点。这两个阶段的求解方法相同。
3. 维护一个栈，栈中记录当前待定的凸包上的点。此时考察一个新的点，记为 c，栈顶倒数第二个点记为 a，栈顶的点记为 b，则 a, b, c 三个点可以构成 a-b 和 a-c 两个线段。
4. 如果 a-c 在 a-b 的右下的方向，则 b 点显然就不是凸包上的点（这里可以自己在纸上画一个图）。判断是否 a-c 在 a-b 的外侧可以用 a-b 与 a-c 的差积是否小于 0 来判断。
5. 这样遍历一次，就做完了第一阶段，栈中的点就是下方和右方的凸包点。接着反向遍历一次，就可以求出上方和左方的凸包点。
6. 注意，此题要求在同一线段上的点都需要记录。为了避免重复的点，可以用集合来维护。

时间复杂度

• 排序的时间复杂度为 $O(n \log n)$。
• 求解凸包的时间复杂度为 $O(n)$。
• 集合去重的时间复杂度为 $O(n \log n)$。
• 故总时间复杂度为 $O(n \log n)$。

空间复杂度

• 需要额外 $O(n)$ 的栈空间，以及 $O(n)$ 的空间记录答案。

C++ 代码

class Solution {
public:
    bool check(const vector<int> &a, const vector<int> &b, const vector<int> &c) {
        int x1 = b[0] - a[0], y1 = b[1] - a[1];
        int x2 = c[0] - a[0], y2 = c[1] - a[1];

        return x1 * y2 - x2 * y1 < 0;
    }

    vector<vector<int>> outerTrees(vector<vector<int>>& points) {
        int n = points.size();
        set<vector<int>> ans;

        sort(points.begin(), points.end());
        vector<vector<int>> st;

        for (int i = 0; i < n; i++) {
            while (st.size() >= 2 && check(st[st.size() - 2], st.back(), points[i]))
                st.pop_back();
            st.push_back(points[i]);
        }

        for (int i = 0; i < st.size(); i++)
            ans.insert(st[i]);

        st.clear();

        for (int i = n - 1; i >= 0; i--) {
            while (st.size() >= 2 && check(st[st.size() - 2], st.back(), points[i]))
                st.pop_back();
            st.push_back(points[i]);
        }

        for (int i = 1; i < st.size() - 1; i++)
            ans.insert(st[i]);

        return vector<vector<int>>(ans.begin(), ans.end());
    }
};