题目描述

给定一张 n 个点的带权无向图，点从 0~n-1 标号，求起点 0 到终点 n-1 的最短Hamilton路径。 Hamilton路径的定义是从 0 到 n-1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数n。

接下来n行每行n个整数，其中第i行第j个整数表示点i到j的距离（记为a[i,j]）。

对于任意的x,y,z，数据保证 a[x,x]=0，a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]>=a[x,z]。

输出格式
输出一个整数，表示最短Hamilton路径的长度。

数据范围
1≤n≤20
0≤a[i,j]≤107

输入样例

5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0

输出样例

18

解题思路

先看个实例。

有5个点， 求其最短哈密顿路径

0 1 2 3 4     

每个点只能经过一次, 对于已经走过的点, 无法影响到后面的点.

对于0 1 2 3 4 来说  假如已经走了  0 1 2  三个点  现在只能走2 -> 3  或者2 ->4 所以对于 0 1 2   = 10   0 2 1 = 20    那么我们一定会舍弃0 2 1 这种情况。如图:

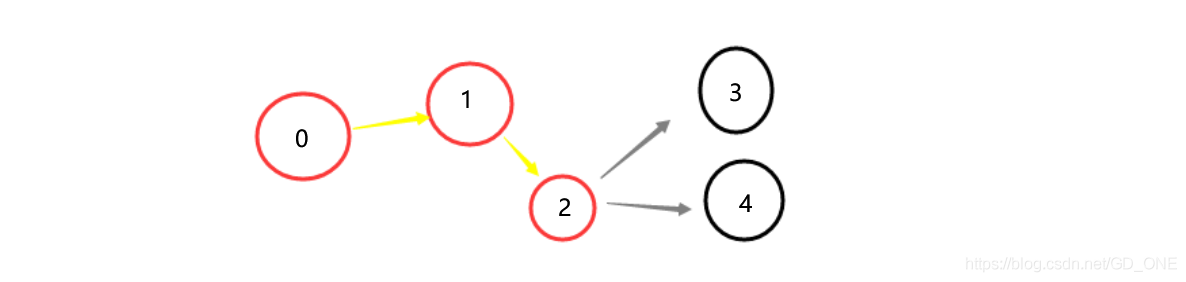
也就是说求最短哈密达路径时  我们只需要保存已经走过的点的最短哈密顿路径！！！以n=3为例，每个点都有两种可能，走或者不走，所以所有的路径情况一共有 2^3种：
0
1
2
0 1
0 2
1 2
0 1 2
还有三个点全都不走的情况, 一共8种。
本题中 n <= 20 所以 最多有2^20种情况需要保存。

对于n=3 来说 要得到走三个点时的最短路径，就要从所有走两个点时的最短路径转移过来。
假如 n == 4   那么  0XX3->4        0XX2->4     0XX1->4 中的最小值也就是答案了.（假如1 2 3号点均可以到达4号点）

即其余4个点都被经过时的最短哈密顿路径。

而对于   0XX3   0XX2  0XX1     0XX 只是一个状态 分别表示经过（012）、（013）、（023）时的最短哈密顿路径.

而所谓的状态压缩就是把 一个状态集合  用 一个二进制数表示。 对于本题来说 0表示不经过， 1表示经过。

如经过了  0 1 3 号点则其最短路径的状态用S = 01011来表示(最高位表示第n号点， 最低位表示0号点。)

所以对于第n号点来说, 只需要求出所有能从n-1个点到达第n个点的最短路径,就能求出到达第n号点的最短路径. 

同样对于一个点i来说, 从其他点到达点i时的最短哈密顿路径就是：

    for(int j = 0; j < n; j++){
        dp[S][i] = min(dp[S][i], dp[S^(1<<i)][j] + weight[j][i]//S^(1<<i)表示没有经过i点时的状态 
    }

（不知道怎么让字体高亮显示，所以显得很乱..将就能看吧。0.0， 我的博客里可能看的更清楚一些博客链接： https://blog.csdn.net/GD_ONE/article/details/103899275)

C++ 代码

#include <iostream>
#include <cstring>
using namespace std;
int dp[1<<20][20];
int weight[20][20];
int main(){        
    int n;              
    cin >> n;      
    for(int i = 0; i < n; i++)     
    for(int j = 0; j < n; j++)
        cin>>weight[i][j];
    memset(dp, 0x3f, sizeof dp);
    dp[1][0] = 0;
    for(int S = 1; S < 1<<n; S++){               
        for(int i = 0; i < n; i++){
            if(S & (1<<i)){ //遍历到了第i个点  此时第i个点的状态为 1 
                for(int j = 0; j < n; j++){  
                    if(S & (1<<j) )  // 第j个点的状态为1   从第j个点到第i个点  所以第j个点一定走过了 第 i 个点一定没有走过。
                        dp[S][i] = min(dp[S][i], dp[S^(1<<i)][j] + weight[j][i]);                       
                }
            }
        }                                              
    }   
    cout<<dp[(1<<n)-1][n-1];   // 注意 - 号优先级大于 <<   所以  (1<<n) - 1 注意括号。
    return 0;
}