题目描述

给你一棵二叉树，请你返回满足该结点的祖父结点的值为偶数的结点的和。（一个结点的 祖父 结点是指该结点的父结点的父结点。）

如果不存在祖父结点值为偶数的结点，那么返回 0 。

样例

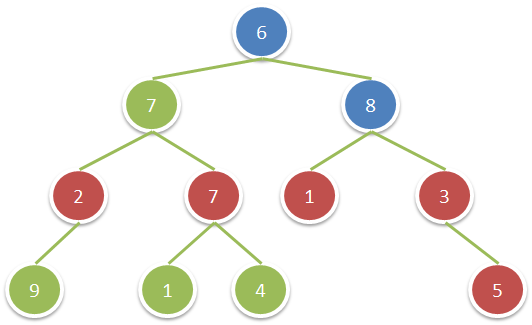
输入：root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
输出：18
解释：图中红色结点的祖父结点的值为偶数，蓝色结点为这些红色结点的祖父结点。

限制

• 树中结点的数目在 1 到 10^4 之间。
• 每个结点的值在 1 到 100 之间。

算法

(递归回溯) $O(n)$

1. 递归遍历整棵树，递归的函数记录当前的父结点和祖父结点。
2. 如果当前结点的祖父结点的值为偶数，则更新答案。然后递归左子结点和右子结点，在递归函数中，将父结点更新到祖父结点上，新的父结点为当前结点。

时间复杂度

• 每个结点仅访问常数次，故时间复杂度为 $O(n)$。

空间复杂度

• 最坏情况下，需要额外 $O(n)$ 的系统栈空间支持递归。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    void solve(TreeNode *r, int &ans, TreeNode *p, TreeNode *gp) {
        if (!r)
            return;

        if (gp && gp -> val % 2 == 0)
            ans += r -> val;

        solve(r -> left, ans, r, p);
        solve(r -> right, ans, r, p);
    }

    int sumEvenGrandparent(TreeNode* root) {
        int ans = 0;

        solve(root, ans, NULL, NULL);

        return ans;
    }
};