算法分析

此题考查树状数组的应用

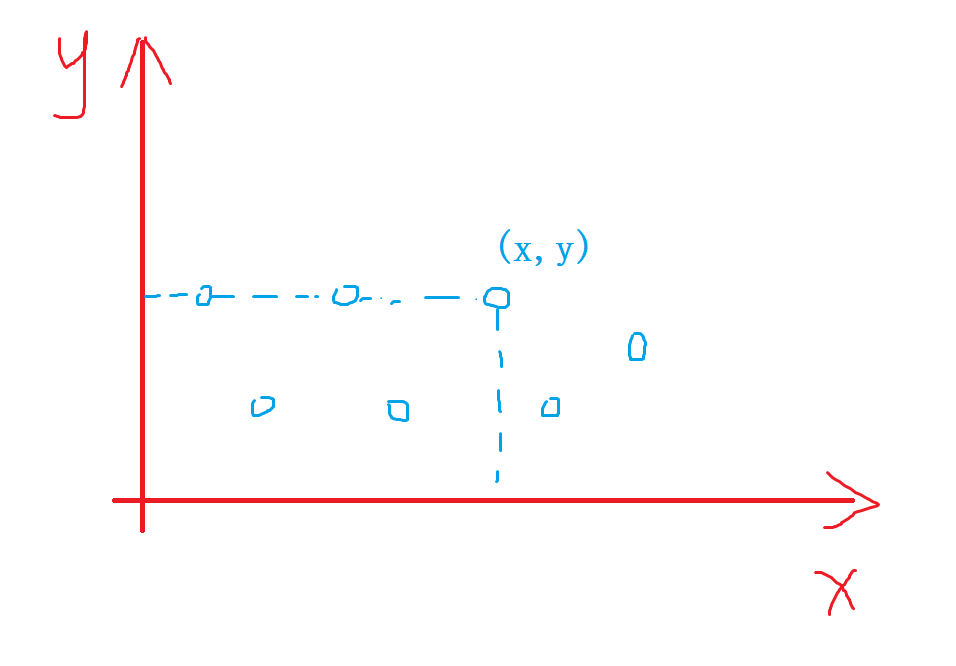
• 1、题目要求求某一个点(x,y)左下方星星的个数(不包括自己)，且星星按y坐标增序给出，y 坐标相同的按x坐标增序给出,因此对于每个新来的点(x,y),y是当前纵坐标的最大值，只需要求[1,x]中星星出现的数量即可

• 2、通过树状数组完成单点修改，区间查询操作

注意：树状数组是从1开始的，而题目的给定的x范围是0≤x≤32000,因此需要将所有的x赋值成x + 1(相对位置不变)

时间复杂度 $O(nlogn)$

参考文献

算法提高课

Java 代码

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    static int N = 32010;
    static int[] a = new int[N];
    static int[] tr = new int[N];
    static int n;
    static int[] level = new int[N];
    static int lowbit(int x)
    {
        return x & -x;
    }
    static void add(int x,int v)
    {
        for(int i = x;i < N;i += lowbit(i)) tr[i] += v;
    }
    static int query(int x)
    {
        int res = 0;
        for(int i = x;i >= 1;i -= lowbit(i)) res += tr[i];
        return res;
    }
    public static void main(String[] args) throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(reader.readLine().trim());
        for(int i = 0;i < n;i++)
        {
            String[] s1 = reader.readLine().split(" ");
            int x = Integer.parseInt(s1[0]) + 1;
            int y = Integer.parseInt(s1[1]);
            level[query(x)] ++;
            add(x,1);
        }
        for(int i = 0;i < n;i++) System.out.println(level[i]);


    }
}