博客园阅读地址

Problem

POJ 题目地址

ACwing 题目地址

题意简述

有一个城镇，是44的大小的，然后你控制一块云彩，22的，你每天可以有9种走的方法，上下左右，或者不动，走的时候可以走1或者2步，云彩所在的地方肯定会下雨，然后给你做多365天的安排，要求某些日子的某些城镇不能下雨（因为有节日），还有任何地方都不能有连续超过6天不下雨。

Solution

一道蛮有意思的搜索题！

首先看到这个题目，肯定会想到直接暴搜，不加任何优化，直接存储状态。这样实现麻烦，时间空间开都销大，不能通过此题。

因此我们要稍作思考。可以发现，我们只要记录4*4城镇的四个角在 6 天内有无降水，就可以判断所有的城镇。换言之，如果四个角合法，那么整张图合法；如果四个角不合法，那么整张图不合法。

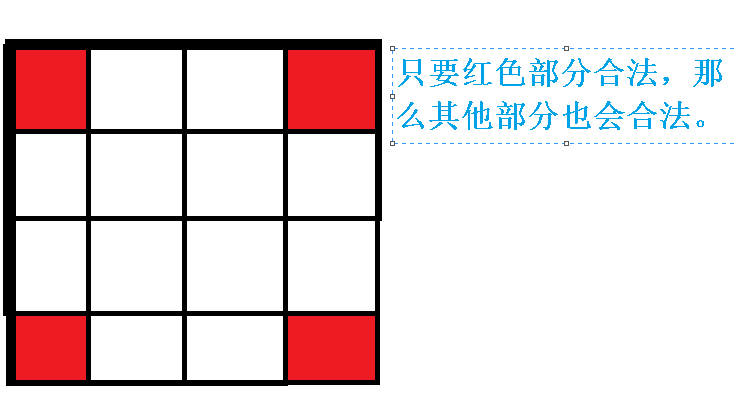
它的充要性很好证明。如果你实在不会那我就说一下qwq

证明 必要性，如果整张图合法，那么这四个角一定合法。 充分性，如果这四个角合法，那么假设这四个角中的某一个角淋到雨的时候，云的左上角坐标是 $(x,y)$（我们用左上角位置来描述一朵云），可以发现，要让这四个角淋到雨，云的坐标必须分别是 $(1,1),(1,3),(3,1),(3,3)$，恰好当云经过了这四个坐标，就覆盖了整个图。

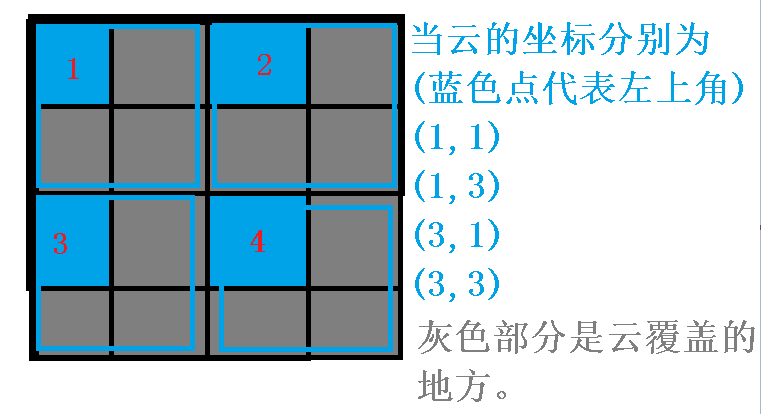
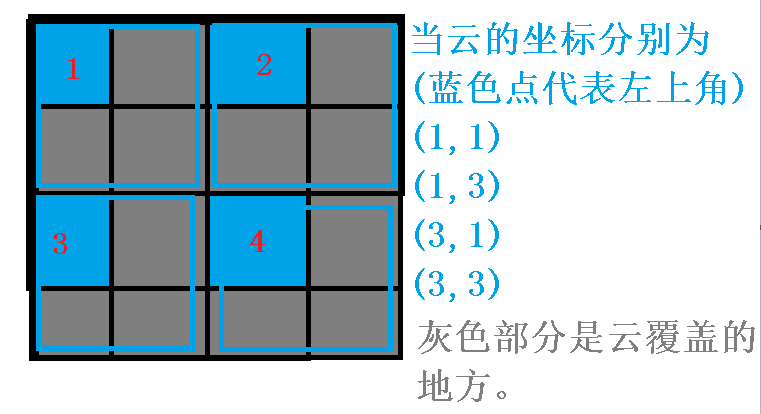
所以我们在判断 “任何地方都不能有连续超过6天不下雨” 可以记录四个角来判断，而不是整张图！！！

现在我们定义 搜索 的框架（状态）：

• 当前天数 （搜索深度）

• 云的位置（左上角坐标 $(x,y)$）

• 四个角的状态（最近的一次下雨是什么时候）

小技巧：

• 把输入 二进制状态压缩 保存起来。

剪枝 / 优化

相信你看到这里头又大了一圈，“怎么又是剪枝啊！！！”。其实是个很简单的啦qwq

• 记忆化保存每个状态，保证每个状态只被搜一次。具体：开一个 $vis[dep][(x,y)][(d1,d2,d3,d4)]$ 数组，记录每个状态是否搜过。回顾我们的状态，$dep$ 表示天数，$(x,y)$ 可以用公式 $x*4+y$ 表示在哪一个，$d$ 就是四个角，我们发现最多离上一次淋雨 6 天，我们的 $d$ 就表示离上一次淋雨几天（和上面的搜索状态有所不同），可以用 七进制状态压缩 储存

至此，我们解决了这个问题。更多实现技巧看代码。复杂度不会超过 $vis[][][]$ 数组的大小（每个状态搜一次）

Code

Talk is cheap.Show me the code.

#include<bits/stdc++.h>
using namespace std;
inline int read() {
    int x=0,f=1; char ch=getchar();
    while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
    return x * f;
}
const int N = 366, M = 10, MAXN = 2807;
const int dx[] = {0,-1,1,0,0,-2,2,0,0};
const int dy[] = {0,0,0,-1,1,0,0,-2,2};
int n;
int state[N];
bool vis[N][M][MAXN];
struct Node {
    int d[4];
}st;
inline int Get(int x,int y) {
    return 1<<(x*4+y);
}
inline bool check(int now,int x,int y,Node cr) {
    for(int i=0;i<4;++i)
        if(now - cr.d[i] > 6) return false;
    int weather = Get(x,y) | Get(x,y+1) | Get(x+1,y) | Get(x+1,y+1);
    if(weather & state[now]) return false;
    int s = 0, base = 8;
    for(int i=0;i<4;++i)
        s = s*base + (now - cr.d[i]);
    if(vis[now][x*4+y][s]) return false;    //记忆化，剪枝 
    return vis[now][x*4+y][s] = true;
}
inline bool valid(int x,int y) {
    return (x>=0&&x<3&&y>=0&&y<3);  //注意下标从 0 开始编号 
}
bool Dfs(int dep,int x,int y,Node cr) { //corner 角落 
    if(!check(dep,x,y,cr)) return false;
    if(dep == n) return true;
    for(int i=0;i<9;++i) {
        int nx = x + dx[i], ny = y + dy[i]; Node ncr = cr;
        if(!valid(nx,ny)) continue;
        if(nx==0 && ny==0) ncr.d[0] = dep + 1;
        if(nx==0 && ny==2) ncr.d[1] = dep + 1;
        if(nx==2 && ny==0) ncr.d[2] = dep + 1;
        if(nx==2 && ny==2) ncr.d[3] = dep + 1;
        if(Dfs(dep+1,nx,ny,ncr)) return true;
    }
    return false;
}
void work() {
    memset(state, 0, sizeof(state));
    memset(vis, 0, sizeof(vis));
    for(int i=1;i<=n;++i)
        for(int j=0;j<16;++j)
            state[i] |= (read()<<j);
    //for(int i=1;i<=n;++i) printf("state[%d] = %d\n",i,state[i]);
    //cout << endl;
    st.d[0] = st.d[1] = st.d[2] = st.d[3] = 0;
    vis[1][1*4+1][0] = 1;
    printf("%d\n",Dfs(1,1,1,st));
    //cout << endl;
}
int main()
{
    while(true) {
        n = read();
        if(!n) break;
        work();
    }
    return 0;
}

Summary

通过这个题目，我学到了：

• 巧妙发现题目性质，简设状态。

• 巧用状压。

• 巧用记忆化，加快程序速度。