算法1

(动态规划) $O(n^2)$

时间复杂度

&O(n)&

C++ 代码

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        for(int i = 1; i<triangle.size(); i++)
            for(int j = 0; j<=i; j++){
                if(j > 0 && j < i) triangle[i][j] += min(triangle[i - 1][j - 1], triangle[i - 1][j]);
                else if(j == 0) triangle[i][j] += triangle[i - 1][j];
                else triangle[i][j] += triangle[i - 1][j - 1];
            }
        int res = INT_MAX;
        for(int i = 0; i <triangle[triangle.size() - 1].size(); i++)
            res = min(res, triangle[triangle.size() - 1][i]);
        return res;
    }
};

直接在triangle上做的。

优化

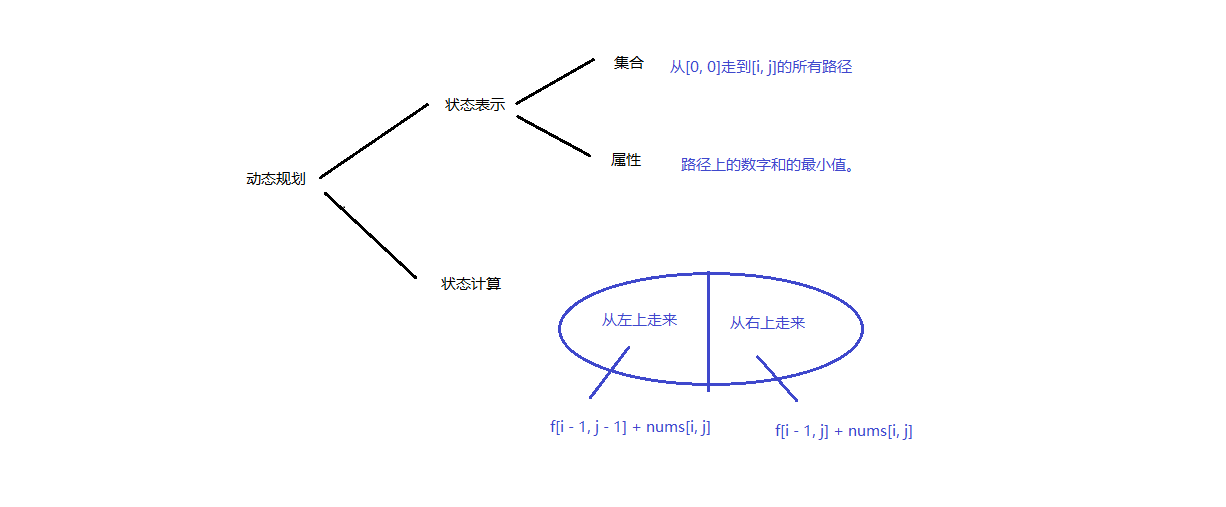
状态转移方程dp[i][j] = min(dp[i - 1][j - 1], dp[i-1][j]) + nums[i][j];
直接去掉一维dp[j] = min(dp[j - 1], dp[j]) + nums[i][j];
可以看到是需要j-1的，所以第二维要从后向前遍历。

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int n = triangle[triangle.size() - 1].size();
        long long  dp[n];

        dp[0] = triangle[0][0];
        for(int i = 1; i<triangle.size(); i++){
            dp[i] = INT_MAX;//每次循环将最后一个设为无穷，处理边界。
            for(int j = triangle[i].size() - 1; j>=0; j--)
                if(j) dp[j] = min(dp[j], dp[j - 1]) + triangle[i][j]; //滚动数组优化
                else dp[j] += triangle[i][j];
        }
        long long  res = INT_MAX;
        for(int i = 0; i<n; i++) res = min(res, dp[i]);
        return res;
    }
};