题目描述

满二叉树 是一类二叉树，其中每个结点恰好有 0 或 2 个子结点。

返回包含 N 个结点的所有可能满二叉树的列表。答案的每个元素都是一个可能树的根结点。

答案中每个树的每个结点都必须有 node.val=0。

你可以按任何顺序返回树的最终列表。

样例

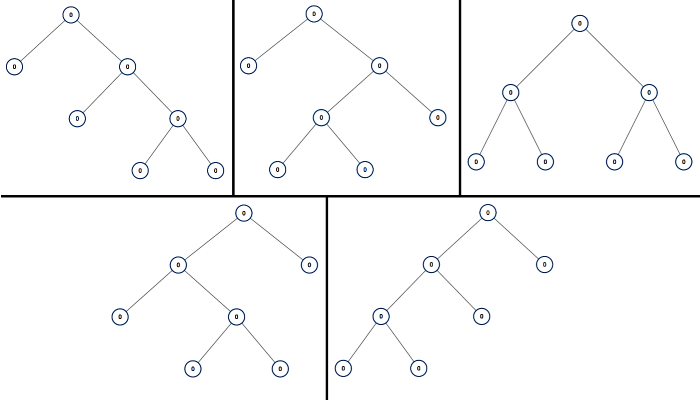
输入：7
输出：[[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],
[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]

注意

• 1 <= N <= 20

算法

(枚举构造) $O(ans.length)$

1. 开一个数组 trees，trees[i] 表示当结点数为 i 个时所有树的树根。当 N 为偶数时答案一定是空。
2. 显然 trees[1] 仅有一种情况。当 i > 1 且为奇数时，trees[i] 可以通过循环枚举计算出来，枚举根结点左子树的结点数 j，然后 trees[j] 和 trees[i - j - 1] 中所有根结点的组合就是 trees[i] 的所有情况。

时间复杂度

• 所枚举的情况数就是答案的个数，故时间复杂度就是 O(答案数)。

空间复杂度

• 同样，每一次枚举都会产生一个新结点，故空间复杂度也是 O(答案数)。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<TreeNode*> allPossibleFBT(int N) {
        if (N % 2 == 0)
            return {};

        vector<TreeNode*> trees[N + 1];
        trees[1].push_back(new TreeNode(0));

        for (int i = 3; i <= N; i += 2) {
            for (int l = 1; l < i - 1; l += 2) {
                int r = i - l - 1;
                for (auto &left : trees[l])
                    for (auto &right : trees[r]) {
                        TreeNode *rt = new TreeNode(0);
                        rt -> left = left;
                        rt -> right = right;
                        trees[i].push_back(rt);
                    }
            }
        }

        return trees[N];
    }
};