题目描述

在 x 轴上有一个一维的花园。花园长度为 n，从点 0 开始，到点 n 结束。

花园里总共有 n + 1 个水龙头，分别位于 [0, 1, ..., n]。

给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges，其中 ranges[i] （下标从 0 开始）表示：如果打开点 i 处的水龙头，可以灌溉的区域为 [i - ranges[i], i + ranges[i]]。

请你返回可以灌溉整个花园的 最少水龙头数目。如果花园始终存在无法灌溉到的地方，请你返回 -1。

样例

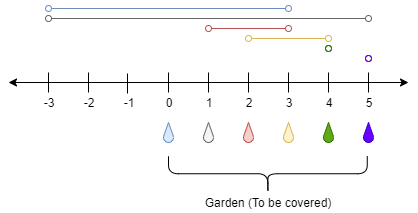
输入：n = 5, ranges = [3,4,1,1,0,0]
输出：1
解释：
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5]

输入：n = 3, ranges = [0,0,0,0]
输出：-1
解释：即使打开所有水龙头，你也无法灌溉整个花园。

输入：n = 7, ranges = [1,2,1,0,2,1,0,1]
输出：3

输入：n = 8, ranges = [4,0,0,0,0,0,0,0,4]
输出：2

输入：n = 8, ranges = [4,0,0,0,4,0,0,0,4]
输出：1

限制

• 1 <= n <= 10^4
• ranges.length == n + 1
• 0 <= ranges[i] <= 100

算法

(贪心) $O(n \log n)$

1. 如果将覆盖区域看做区间，且左端点最小为 0，右端点最大为 n，则此题可以看做区间覆盖问题，即选择最少的区间，覆盖整个区域。
2. 一个贪心做法是，将区间按照左端点排序，同时维护一个当前覆盖到的最大位置 end。
3. 初始时，end 为 0，我们在左端点小于等于 end 的线段里挑选一个区间，满足新的 next_end 尽可能大。用 next_end 来更新 end 然后进行下一轮挑选。
4. 如果发现挑选过后 end 和 next_end 相等，则说明无法继续挑选下一个区间满足左端点小于等于 end（即连续覆盖）。

时间复杂度

• 排序后仅需要线性扫描，故时间复杂度为 $O(n \log n)$。

空间复杂度

• 需要额外 $O(n)$ 的空间记录区间。

C++ 代码

class Solution {
public:
    int minTaps(int n, vector<int>& ranges) {
        vector<pair<int, int>> p(n + 1);
        for (int i = 0; i <= n; i++)
            p[i] = make_pair(max(0, i - ranges[i]), min(n, i + ranges[i]));

        sort(p.begin(), p.end());

        int i = 0, end = 0, ans = 0;
        while (i <= n && end < n) {
            int next_end = 0;
            while (i <= n && p[i].first <= end) {
                next_end = max(next_end, p[i].second);
                i++;
            }

            if (end == next_end)
                return -1;

            ans++;
            end = next_end;
        }

        return ans;
    }
};