题目描述

给定一个二叉树（具有根结点 root），一个目标结点 target，和一个整数值 K。

返回到目标结点 target 距离为 K 的所有结点的值的列表。答案可以以任何顺序返回。

样例

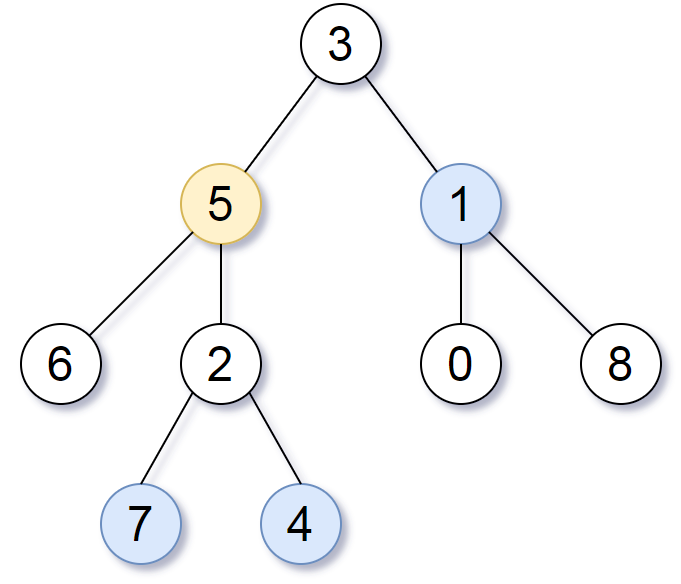
输入：root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2

输出：[7,4,1]

解释：
所求结点为与目标结点（值为 5）距离为 2 的结点，
值分别为 7，4，以及 1

注意，输入的 "root" 和 "target" 实际上是树上的结点。
上面的输入仅仅是对这些对象进行了序列化描述。

注意

• 给定的树是非空的。
• 树上的每个结点都具有唯一的值 0 <= node.val <= 500。
• 目标结点 target 是树上的结点。
• 0 <= K <= 1000。

算法

(深度优先遍历) $O(n)$

1. 我们需要做若干次深度优先遍历。
2. 第一次需要定位 target 的具体位置，并按顺序记录其到根结点的路径。路径中的每个点，用一个二元组表示，分别为点的指针，和一个布尔值。其中布尔值为 true 代表 target 是在当前结点的左侧，否则在右侧。路径不包括 target 本身。
3. 然后，我们顺着路径，从底向上。如果路径上当前的点已经和 target 距离为 K，则保存当前结点，然后退出循环。否则，如果布尔值为 true，则从右侧开始深度优先遍历找距离 target 为 K 的结点，否则从左侧开始找。
4. 最后，从 target 开始深度优先遍历找答案。

时间复杂度

• 第一次深度优先遍历每个结点最多遍历一次，故时间复杂度为 $O(n)$。
• 从路径上的结点开始做的深度优先遍历，并不会重复访问一个结点多次，与最后从 target 开始的遍历也不会重复，故总时间复杂度仍然为 $O(n)$。

空间复杂度

• 需要一个数组来保存答案，空间可能达到 $O(n)$。此外，需要 $O(h)$ 的空间来保存路径，以及需要 $O(h)$ 的空间给系统栈使用。故总空间复杂度为 $O(n)$。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    void find(TreeNode *rt, int cur, int K, vector<int>& ans) {
        if (rt == nullptr || cur > K)
            return;
        if (cur == K) {
            ans.push_back(rt -> val);
            return;
        }
        find(rt -> left, cur + 1, K, ans);
        find(rt -> right, cur + 1, K, ans);
    }

    bool findTarget(TreeNode *rt, TreeNode *target, vector<pair<TreeNode*, bool>>& path) {
        if (rt == nullptr)
            return false;
        if (rt == target)
            return true;

        if (findTarget(rt -> left, target, path)) {
            path.emplace_back(make_pair(rt, true));
            return true;
        }
        if (findTarget(rt -> right, target, path)) {
            path.emplace_back(make_pair(rt, false));
            return true;
        }
        return false;
    }

    vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {
        vector<pair<TreeNode*, bool>> path;
        findTarget(root, target, path);
        vector<int> ans;

        for (int i = 0; i < path.size(); i++) {
            if (i + 1 == K) {
                ans.push_back(path[i].first -> val);
                break;
            }
            if (path[i].second == true)
                find(path[i].first -> right, i + 2, K, ans);
            else
                find(path[i].first -> left, i + 2, K, ans);
        }

        find(target, 0, K, ans);
        return ans;
    }
};