完全背包做法

 原题目题意就是从 1 ~ n 中选选任意个数 组成 n 也就是说从 1 ~ i 中选任意个数加起来等于j; 
 所以这个题就为完全背包问题的变式! 
 f[i][j] 的状态表示: i 为 从 1 ~ i 中选 总体积恰好为 j
 f[i][j] 的性质 : 数量;
 f[i][j] 的计算: 第i个物品选k个;
f[i][j] = f[i-1][j] + f[i-1][j-i] + f[i-1][j - i*2] + ....f[i-1][j-i*s];
f[i][j - i] =         f[i-1][j-i] + f[i-1][j - i*2] + ....f[i-1][j-i*s];
合并一下 f[i][j] = f[i-1][j] + f[i][j-i];
优化成一维 f[j] = f[j] + f[j-i];

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e4+7 , mod = 1e9+7;
int f[N];
int main()
{
    int n ; scanf("%d",&n);
    f[0] = 1; // 一个都不选的情况下 而且体积 为0 所以 数量只有一个;
    // 比如f[1] , 表示一个都不选 但是体积为 1 的时候 所以一定为 0;
    for(int i = 1 ; i <= n ; i++)  
        for(int j = i ; j <= n; j++) // 完全背包用不到i - 1 层 从小到大枚举体积就OK 
            f[j] = (f[j]+f[j-i]) % mod;

    cout << f[n] << endl;
    return 0;
}

非背包问题做法

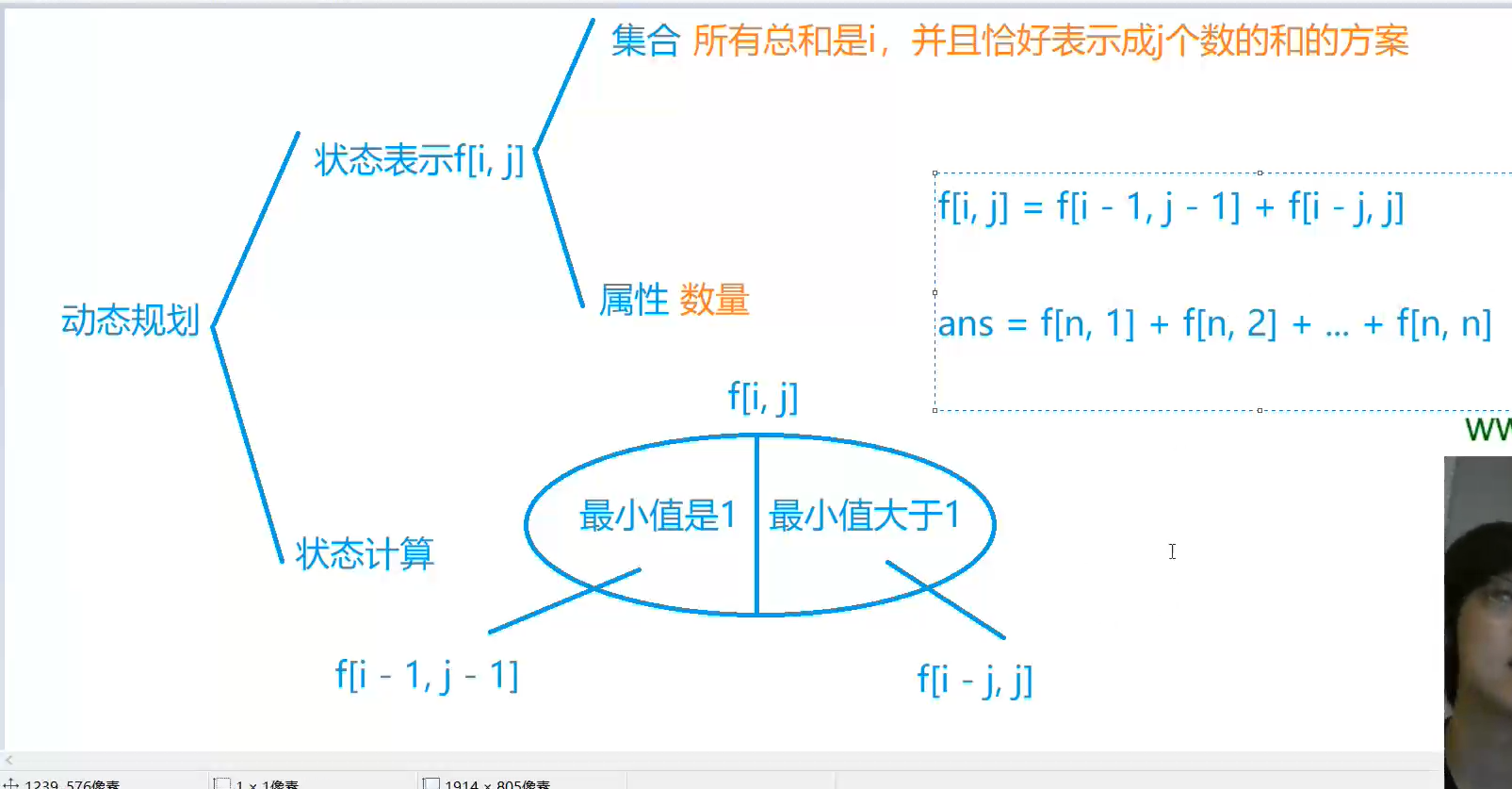
PS : 最小值1 表示 组成 总和是 i 的里面最小的数为1

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e4+7,mod = 1e9+7;
int f[N][N];
int main()
{
    int n; scanf("%d",&n);
    f[0][0] = 1;
    for(int i = 1 ; i <= n ;i++)
        for(int j = 1; j <= i; j++)
            f[i][j] = (f[i-1][j-1] + f[i-j][j]) % mod;

    int res = 0;
    for(int i = 1 ; i <= n ; i++) res =(res + f[n][i]) % mod;
    cout << res << endl;
    return 0;
}