对于 蒙德里安的梦想 一题的说明

==该题的核心在于，总方案数等于只放横着的小方块的合法的方案数。==

f[i, j]表示从第i - 1列横向伸出到第i列,状态是j的方案数。

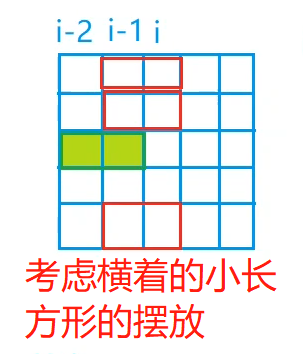
在这里我们看一个具体的例子来感受一下：

• f[i-1,k]，其中的k是如上所示的绿色方格的摆放方案，代表从i-2列伸向i-1列的摆放方案是00100。
• f[i,j]，其中的j是如上所示的红色方格的摆放方案，代表从i-1列伸向i列的摆放方案是11001。

f[i, j]的i是从0开始的，0是第一列，m - 1是最后一列，所以f[m, 0]是指第m - 1列摆满（m-1列伸向第m列的方格数为0）的方案数。

时间复杂度分析

状态表示：该题是二维状态，横行的最大状态数是11，竖行的最大状态数是2^11。

状态计算：最大状态数也是2^11，从i-1列伸向i列每一行都有伸或者不伸两种选择。

因此总的时间复杂度就是 11 * 2^11 * 2^11。

代码及详细注释

#include<iostream>
#include<cstring>
using namespace std;

typedef long long LL;
const int N=12,M=1<<N;
int n,m;//宽，长
long long f[N][M];//DP矩阵，可能方案数会很大因此，使用long long 来保存里面的方案数
bool st[M];//里面保存的是,i-1列到i列的状态j是否合乎要求（即没有连续的空白格）

int main(){

    while(scanf("%d%d",&n,&m)!=EOF,n||m){//，运算符最终将n||m的值作为条件判定的条件
        //预处理部分
        for(int i=0;i<1<<n;i++){//枚举状态
            st[i]=true;
            int cnt=0;
            for(int j=0;j<n;j++){//状态中的二进制位
                if(i>>j&1){
                    if(cnt%2){
                        st[i]=false;

                    } 
                    cnt=0;
                }else{
                    cnt++;
                }
            }
            if(cnt%2) //最后一段二进制位0的个数是否为奇数
                st[i]=false;
        }
        memset(f,0,sizeof f);//新的输入新的状态
        //动态规划部分
        f[0][0]=1;//一个横行都不放也是一种状态
        for(int i=1;i<=m;i++){//枚举列
            for(int j=0;j<1<<n;j++){//枚举i-2列到i-1列的方案数j
                for(int k=0;k<1<<n;k++){//枚举i-1列到第i列的方案数k
                    if(!(j&k)&&st[j|k]){//如果添加k方案之后和j方案有重叠部分，或者添加k方案之后使得i-1列有奇数空白格则为不合法
                        f[i][k]+=f[i-1][j];
                    }
                }
            }
        }

        printf("%ld\n",f[m][0]);//0~m-1列为需要填入方块的列，m列不应该有任何的m-1列的长方形伸过来，此时即最终所有的方案数

    }


    return 0;
}