问题链接

最长上升子序列 II

基本思路

这道题做得我挺蒙蔽的，看了 yls 的视频之后自己又想了一下，还是写篇题解。

首先，求最长上升子序列（后面称 LIS ）的问题和它的子问题有这样的依赖关系：

上图这样就可以求得序列3 1 2 1 8 5 6的 LIS 长度是 4 ，把6接在1 2 5后面即可。
所以，要求串a[0...i]的 LIS ，就要知道：串a[0...i-1]中各长度的上升子序列末尾元素的最小值。

后者可以用一个q数组来存储，q[i]是所有长度为i的上升子序列末尾元素的最小值。这个数组是严格单调递增的（原因不赘述），所以每次只要用二分查找，在$O(logn)$的时间内就能从串a[0...i-1]对应的p数组求得串a[0...i]的 LIS ，完成状态转移。

q 数组的维护

接下来的难题就是如何在求得串a[0...i]的 LIS 后更新q数组，好让下一个到串a[0...i+1]的状态转移顺利发生。在下面的代码里面可以看到，实际上在每轮循环只需要做一件事：将本次发现的 LIS 的末尾元素赋值给q[l+1]。为什么这么简单？有两点问题：

1. 注意这里是直接赋值，而不是求min，为什么a[i]一定不大于q[l+1]？
2. 为什么只修改q[l+1]这一项？其他项一定不需要更新吗？

画个图（1.）就很清楚了，由于我们是二分搜索搜到的l，所以a[i]一定是严格大于q[l]，而小于等于q[l+1]。

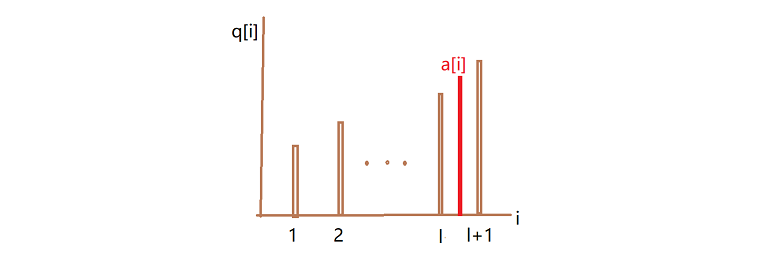
对于（2.），首先由于当前串的 LIS 长度就只有l+1，所以q[l+1]后面的项肯定不会被更新。对于q[1...l]，看这个例子就很容易明白了：

PS：
这个问题里面的贪心思想我还没捋明白，不过我贪心的课还没听，说不定以后会回来更新一下。

参考文献

y老师 算法基础课 week8习题课

代码

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;
int n, a[N], q[N];
int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    q[0] = -INF; // 省得考虑边界
    int len = 0;
    for (int i = 0; i < n; i++) { // 从短到长解决各个子串的 LIS
        int l = 0, r = len; // 二分搜索，得到能接在 a[i] 前面的上升子序列的最大长度 l
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (q[mid] < a[i]) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        len = max(len, l + 1);
        q[l + 1] = a[i];
    }
    cout << len << '\n';
    return 0;
}