题目描述

大家都知道 Fibonacci 数列吧，f1=1,f2=1,f3=2,f4=3,…,fn=fn−1+fn−2。

现在问题很简单，输入 n 和 m，求 fn 的前 n 项和 Snmodm。

输入格式
共一行，包含两个整数 n 和 m。

输出格式
输出前 n 项和 Snmodm 的值。

数据范围
1≤n≤2000000000,
1≤m≤1000000010a

样例

输入样例：
5 1000
输出样例：
12a

(快速冥+矩阵优化) $O(3^3*1ogn)$

朴素算法虽然是O(n)的，但本题的数据范围已经超过了10的九次方，显然会超时，所以我们可以构造一个矩阵来优化。
我们知道一个nm的矩阵只能与一个mr的矩阵相乘，即C[i][j] = A[i][1~m] * B[1~m][j]，两两相乘然后在相加，
以此类推得出一个n*r的矩阵。

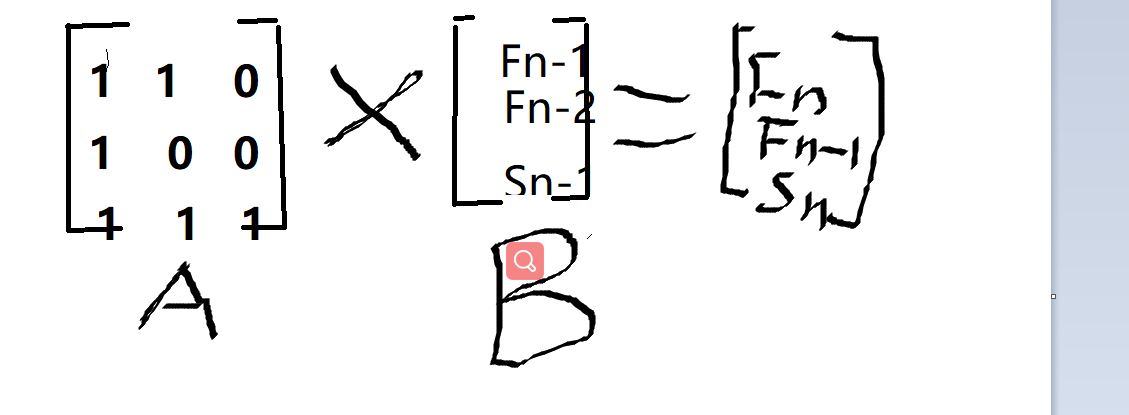
如上图所示

Fn = 1*Fn-1 + 1*Fn-2 + 0 * Sn-1 
Fn-1 = 1 * Fn-1 + 0 * Fn-2 + 0 * Sn-1
Sn = 1*Fn-1 + 1*Fn-2 + 1 * Sn-1 = Fn + Sn-1 

像这样每次与构造出来的矩阵A相乘即可得到数列下一项，既矩阵A^n-1 * B 等于数列的第n+1项,然而这还远远不够，矩阵相乘也会耗费大量的时间。
所以我们采用快速幂的思想，使矩阵相乘的时间复杂度降至O(logn)级别。
具体请看代码实现，此处不做过多赘述~~

时间复杂度

矩阵快速幂复杂度为$O(1ogn)$,矩阵相乘为$O(3^3)$,所以复杂度为$O(3^3*1ogn)$。

可以说这个算法效率极高了。

C++ 代码

#include<iostream>
#include<cstring>
using namespace std;
typedef long long LL;
struct matrix{LL data[4][3] = {1,1,0,1,0,0,1,1,1};};

int n,m;

matrix mul(matrix a,matrix b){
    matrix c;
    memset(c.data,0,sizeof(c.data));


    for(int i = 0 ; i < 3 ; i++)
        for(int j = 0 ; j < 3 ; j++)
            if(a.data[i][j])
                for(int k = 0 ; k < 3 ; k++)
                    c.data[i][k] = (c.data[i][k] + 1ll*a.data[i][j]*b.data[j][k]%m)%m;


    return c;
}

matrix mul1(matrix a,int b[4][1]){
    matrix c;
    memset(c.data,0,sizeof(c.data));


    for(int i = 0 ; i < 3 ; i++)
        for(int j = 0 ; j < 3 ; j++)
            if(a.data[i][j])
                for(int k = 0 ; k < 1 ; k++)
                    c.data[i][k] = (c.data[i][k] + 1ll*a.data[i][j]*b[j][k]%m)%m;


   return c;
}

matrix quickpow(matrix a,int k){
     matrix c;

     memset(c.data,0,sizeof(c.data));
    for(int i = 0 ; i < 3 ; i++)
        c.data[i][i]  = 1 ;
    while(k)
    {
        if(k&1)c = mul(c,a);
        k>>=1;
        a = mul(a,a);
    }


    return c;
}

int main(){
    cin>>n>>m;
    matrix a;
    int fib[4][1] = {1,0,1};
    if(n!=1)   // 需要特判，当n为1时间不需要计算直接输出结果即可
    {
        matrix ans = quickpow(a,n-1);
        ans = mul1(ans,fib);
        cout<<ans.data[2][0]<<endl;  
    }
    else cout<<1<<endl;



    return 0;
}