AcWing 255. 第 k 小数    原题链接    简单

作者： 作者的头像   Lemmon_kk ,  2020-07-10 11:06:48 ,  所有人可见 ,  阅读 1411

7


1

整体二分（值域）

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 100010 + 10010;

int n, m;
int tr[N];
struct Node{
    int op; // op = 1 insert // op = 2 query
    int x, y, k;
    int id;// 第几个询问 ans[id];
    Node(int op = 0, int x = 0, int y = 0,int k = 0,int id = 0)
        :op(op), x(x), y(y), k(k), id(id){}
}q[N], lq[N], rq[N];
int ans[N];

// 树状数组 维护
int lowbit(int x){
    return x & -x;
}

void updata(int x,int v){
    for(;x <= n;x += lowbit(x)) tr[x] += v;
}

int query(int x){
    int res = 0;
    for(;x;x -= lowbit(x)) res += tr[x];
    return res;
}

void solve(int vl,int vr,int ql,int qr){
    // 防止re
    if(ql > qr || vl > vr) return ;

    // 如果vl == vr 则 [ql, qr] 所有查询操作的 ans 为 qr
    if(vl == vr){
        for(int i = ql;i <= qr;i ++ )
            if(q[i].op == 2)
                ans[q[i].id] = vr;
        return ;
    }

    // mid 二分 [vl, mid] -> update至树状数组中
    int mid = vl + vr >> 1;
    int nl = 0,nr = 0;
    for(int i = ql;i <= qr;i ++ ){
        if(q[i].op == 1){
            if(q[i].x <= mid){
                updata(q[i].y, 1);
                lq[ ++ nl] = q[i];
            }
            else rq[ ++ nr] = q[i];
        }else{
            int n = query(q[i].y) - query(q[i].x - 1);
            if(n >= q[i].k){
                lq[ ++ nl] = q[i];
            }
            else {
                q[i].k -= n;
                rq[ ++ nr] = q[i];
            }
        }
    }

    // 清空 树状数组
    for(int i = ql;i <= qr;i ++ )
        if(q[i].op == 1)
            if(q[i].x <= mid)
                updata(q[i].y, -1);


    for(int i = 1;i <= nl;i ++ ) q[ql + i - 1] = lq[i];
    for(int i = 1;i <= nr;i ++ ) q[ql + nl + i - 1] = rq[i];

    // 递归 分治左右两边
    solve(vl, mid, ql, ql + nl - 1);
    solve(mid + 1, vr, ql + nl, qr);
}

int main(){

    // 位置一定要 插入在前 查询在后
    scanf("%d%d", &n, &m);
    for(int i = 1;i <= n;i ++ ){
        int x;
        scanf("%d", &x);
        // 在第 i 个位置插入 x
        q[i] = Node(1, x, i);
    }

    int l, r, k;
    for(int i = 1;i <= m;i ++ ){
        scanf("%d%d%d", &l, &r, &k);
        q[i + n] = Node(2, l, r, k, i);
    }

    // 整体二分  值域二分
    solve(-1e9, 1e9, 1, n + m);

    for(int i = 1;i <= m;i ++ ) printf("%d\n", ans[i]);
    return 0;
}

参考 wzc大佬 的做法： orz

wzc 大佬的 这个 是跑的最快的 sto
我写的这样会多开两倍空间，可以参考wzc大佬利用快排的思想，每次交换 就可以省区空间跑的更快一些

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 100010, M = 50010;

int n, m;
struct A{
    int id, x;
}a[N];

struct Q{
    int id;
    int l, r, k;
}q[M], lq[M], rq[M];

int tr[N], ans[M];

inline bool cmp(const A &p, const A &q) {
    return p.x < q.x;
}

inline int lowbit(int x){ return x & -x; }

inline int query(int x) {
    int res = 0;
    for (; x; x -= lowbit(x))
        res += tr[x];
    return res;
}

inline void update(int x, int v) {
    for (; x <= n; x += lowbit(x))
        tr[x] += v;
}

void solve(int L, int R, int l, int r) {
    if (l > r || L > R) return ;

    if (L == R) {
        for(int i = l; i <= r; i ++ )
            ans[q[i].id] = a[L].x;
        return ;
    }

    int mid = (L + R) >> 1;

    for (int i = L; i <= mid; i ++ )
        update(a[i].id, 1);

    int t;
    int nl = 0, nr = 0;

    for(int i = l;i <= r;i ++ ){
        t = query(q[i].r) - query(q[i].l - 1);
        if(q[i].k <= t) lq[ ++ nl] = q[i];
        else{
            q[i].k -= t;
            rq[ ++ nr] = q[i];
        }
        // i -- , j ++ ;
    }

    for (int i = L; i <= mid; i ++ )
        update(a[i].id, -1);

    for(int i = 1;i <= nl;i ++ ) q[i + l - 1] = lq[i];
    for(int i = 1;i <= nr;i ++ ) q[i + l + nl - 1] = rq[i];
    solve(L, mid, l, nl + l - 1);
    solve(mid + 1, R, nl + l, r);
}

int main() {

    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        a[i].id = i;
        scanf("%d", &a[i].x);
    }

    for (int i = 1; i <= m; i++) {
        q[i].id = i;
        scanf("%d%d%d", &q[i].l, &q[i].r, &q[i].k);
    }

    sort(a + 1, a + 1 + n, cmp);

    solve(1, n, 1, m);

    for (int i = 1; i <= m; i++)
        printf("%d\n", ans[i]);

    return 0;
}

省去 两倍空间的写法

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 100010, M = 50010;

int n, m;

struct A {
    int id, x;
}a[N];

struct Q {
    int id;
    int l, r, k;
}q[M];

int f[N], ans[M];

inline bool cmp(const A &p, const A &q) {
    return p.x < q.x;
}

inline int query(int x) {
    int res = 0;
    for (; x; x -= x & -x)
        res += f[x];

    return res;
}

inline void update(int x, int y) {
    for (; x <= n; x += x & -x)
        f[x] += y;
}

void solve(int L, int R, int l, int r) {
    if (l > r)
        return;

    if (L == R) {
        for (int i = l; i <= r; i++)
            ans[q[i].id] = a[L].x;
        return;
    }

    int mid = (L + R) >> 1;

    for (int i = L; i <= mid; i++)
        update(a[i].id, 1);

    int i = l, j = r, t;

    while (i <= j) {
        while (i <= j && q[i].k <= query(q[i].r) - query(q[i].l - 1))
            i++;

        while (i <= j && q[j].k > (t = query(q[j].r) - query(q[j].l - 1))) {
            q[j].k -= t;
            j--;
        }

        if (i < j)
            swap(q[i], q[j]);
    }

    for (int i = L; i <= mid; i++)
        update(a[i].id, -1);

    solve(L, mid, l, j);
    solve(mid + 1, R, i, r);
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        a[i].id = i;
        scanf("%d", &a[i].x);
    }

    for (int i = 1; i <= m; i++) {
        q[i].id = i;
        scanf("%d%d%d", &q[i].l, &q[i].r, &q[i].k);
    }

    sort(a + 1, a + 1 + n, cmp);

    solve(1, n, 1, m);

    for (int i = 1; i <= m; i++)
        printf("%d\n", ans[i]);

    return 0;
}

主席树 (多棵权值线段树)

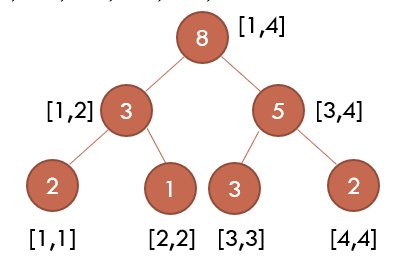
权值线段树
1.png
普通的主席树
2.png
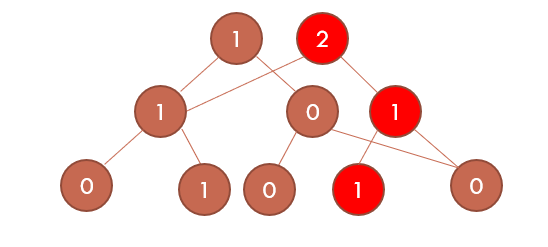
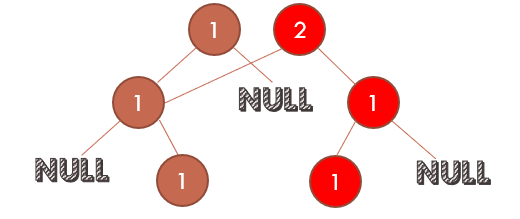
省空间后的主席树
3.png
以下用的是省空间后的主席树

#include <iostream>
#include <ctime>
#include <cstdio>
#include <cctype>
#include <vector>
#include <algorithm>

using namespace std;

const int N = 2e5 + 5;

int n, m;
int a[N];
vector<int> v;
struct Node{
    int l, r, sum;
}hjt[N * 40];
int cnt, root[N];

inline int getid(int x) { return lower_bound(v.begin(),v.end(),x)-v.begin()+1; }

// 插入pre 是历史版本 now 是当前版本  插入p
void insert(int l,int r,int pre,int &now,int p){
    hjt[now = ++ cnt] = hjt[pre];
    hjt[now].sum ++ ;

    if(l == r) return ;
    int mid = l + r >> 1;
    if(p <= mid) insert(l, mid, hjt[pre].l, hjt[now].l, p);
    else insert(mid + 1, r, hjt[pre].r, hjt[now].r, p);
}

int query(int l,int r,int L,int R,int k){
    if(l == r) return r;
    int mid = l + r >> 1;
    int tmp = hjt[hjt[R].l].sum - hjt[hjt[L].l].sum;
    if(k <= tmp) return query(l, mid, hjt[L].l, hjt[R].l, k);
    else return query(mid + 1, r, hjt[L].r, hjt[R].r, k - tmp);
}

int main(){

#ifndef ONLINE_JUDGE
    freopen("D:\\in.in", "r", stdin);
    freopen("out.out", "w", stdout);
#endif

    clock_t c1 = clock();

    scanf("%d%d", &n, &m);

    // 先 离散化
    for(int i = 1;i <= n;i ++ ){
        scanf("%d", &a[i]);
        v.push_back(a[i]);
    }

    sort(v.begin(), v.end());
    v.erase(unique(v.begin(), v.end()), v.end());
    for(int i = 1;i <= n;i ++ )
        insert(1, n, root[i - 1], root[i], getid(a[i]));

    while(m -- ){
        int l, r, k;
        scanf("%d%d%d", &l, &r, &k);
        printf("%d\n", v[query(1, n, root[l - 1], root[r], k) - 1]);
    }

    // fflush(stdin);
    // cout << "Time:" << clock() - c1 << endl;

    return 0;
}

1 评论

用户头像
牛牛蒟蒻   2020-11-01 00:27         踩      回复

666