题目描述

一颗树有 n 个节点，这些节点被标号为：1,2,3…n，每个节点 i 都有一个权值 A[i]。

现在要把这棵树的节点全部染色，染色的规则是：

根节点R可以随时被染色；对于其他节点，在被染色之前它的父亲节点必须已经染上了色。

每次染色的代价为$T*A[i]$，其中T代表当前是第几次染色。

求把这棵树染色的最小总代价。

输入格式
输入中可能包含多组测试用例。

对于每个测试用例，第一行包含两个整数 n 和 R ，分别代表树的节点数以及根节点的序号。

第二行包含 n 个整数，代表所有节点的权值，第 i 个数即为第 i 个节点的权值 A[i]。

接下来n-1行，每行包含两个整数 a 和 b ，代表两个节点的序号，两节点满足关系： a 节点是 b 节点的父节点。

除根节点外的其他 n-1 个节点的父节点和它们本身会在这 n-1 行中表示出来。

同一行内的数用空格隔开。

当输入n=0,R=0的用例时，代表输入结束，且该用例不用被处理。

输出格式
输出一个整数，代表把这棵树染色的最小总代价。

数据范围
$1≤n≤1000$
$1≤A[i]≤1000$

样例

输入样例：
5 1
1 2 1 2 4
1 2
1 3
2 4
3 5
0 0
输出样例：
33

贪心+树上操作+并查集思想+模拟性质

解题思路:首先这道有一个错误的思想,那就是看当前节点的子节点,选择最大的那个节点,这个明显是错误的,如下图所示.

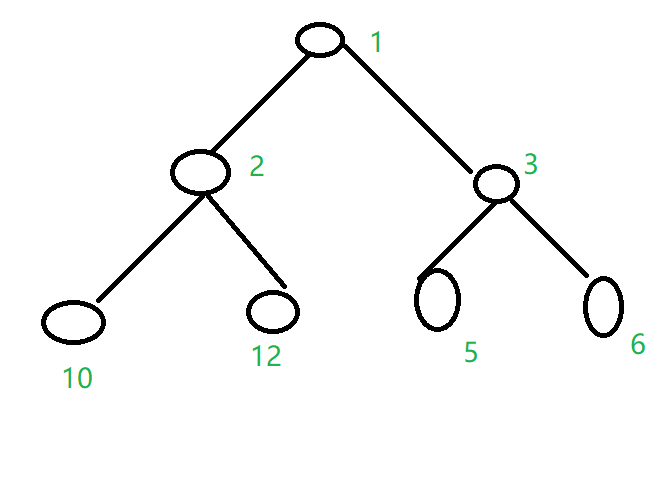
如果按照上面的错误贪心实现肯定是错误的.

下面是正确贪心思路

我们知道,我们肯定是要权值$val$最大的点$x$,越先被染色越好,这是正确的贪心.那么我们怎么染色呢?如果说我们要让$x$点染色的话,那么肯定它的父亲$father[x]$必须先被染色.既然如此的话,那么我们接着可以这样思考.

我们现在面临两个分支,如上图中的根节点1,到底选择2分支,还是3分治的时候.我们发现自然是选择2好,但是计算机不知道,那么如何让计算机知道了,我们可以设置一个数组$w$,设$w[x]$表示为x为根节点的树的平均权值,也就是$w[x]=$x子树的权值总和/x子树的个数.

C++ 代码

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define fir(a,b,c) for (ll a=b;a<=c;a++)
const int N=1010;
ll n,m,r,ans,x,y,now,father;
struct node
{
    ll fa,c,t;
    double w;
} a[N];
ll find()
{
    double maxn=0;
    ll ans=0;
    fir (i,1,n)
        if (i!=r && maxn<a[i].w)
        {
            maxn=a[i].w;
            ans=i;
        }
    return ans;
}
int main()
{
    while(cin>>n>>r && (n || r))
    {
        ans=0;
        fir(i,1,n)
        {
            cin>>a[i].c;
            a[i].w=a[i].c;
            a[i].t=1;
            ans+=a[i].c;
        }
        fir(i,1,n-1)
        {
            cin>>x>>y;
            a[y].fa=x;
        }
        fir (i,1,n-1)
        {
            now=find();
            a[now].w=0;
            father=a[now].fa;
            ans+=a[now].c*a[father].t;
            fir (j,1,n)
                if (a[j].fa==now)
                    a[j].fa=father;
            a[father].c+=a[now].c;
            a[father].t+=a[now].t;
            a[father].w=(double)(a[father].c)/a[father].t;
        }
        cout<<ans<<endl;
    }
    return 0;
}