题目描述

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图，矩形的宽度都为1：

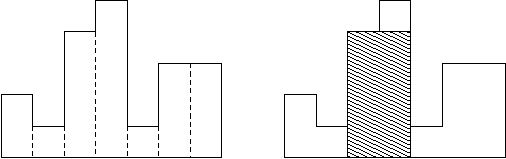
通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式
输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数n开始，表示组成直方图的矩形数目。

然后跟随n个整数$h_1，…，h_n$。

这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为1。

同行数字用空格隔开。

当输入用例为$n=0$时，结束输入，且该用例不用考虑。

输出格式
对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围
$1≤n≤100000, 0≤h_i≤1000000000$

样例

输入样例：
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
输出样例：
8
4000

单调栈

这道题目是一道单调栈的好题目,首先我们要明白什么是单调栈,单调栈如同起名字,就是具有单调性的一个栈,每次读入一个数,如果这个数放入栈中,不满足单调性,那么就要不断地弹出栈顶,直到满足单调性.这就是单调栈的简略操作,那么这道题目是如何利用单调栈的呢?

我们发现,如果说我们确定了这个矩阵的高度的话,那么其实这个矩阵已经确定了,他的$[l,r]$其实我们已经求出来了,因为矩阵要最大,所以贪心求出$l$,$r$即可,那么我们就可以以这个矩阵的高度为单调性,然后每一次弹出的时候,就计算出矩阵的面积,然后开一个ans记录最大值就好了.

我的代码没有用stack,是因为想自己尝试尝试写,毕竟有的时候没有开O2,是会被卡常的.因为作者不是卡常国国王,是常数国国王,自带超大常数

C++ 代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=100005;
ll q[N],w[N],h,n;
int main()
{
    ios::sync_with_stdio(false);
    while(cin>>n && n)
    {
        memset(q,-1,sizeof q);
        int top=0;
        ll ans=0;
        for(int i=1; i<=n+1; i++)
        {
            if(i!=n+1)
                cin>>h;
            else
                h=0;
            if(h>q[top])
                q[++top]=h,w[top]=1;
            else
            {
                ll cnt=0;
                while(h<=q[top])
                {
                    ans=max(ans,(w[top]+cnt)*q[top]);
                    cnt=cnt+w[top--];
                }
                q[++top]=h;
                w[top]=cnt+1;
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}