关键：

确定能否形成U形槽，
更新槽的底部，
用木桶效应确定木桶能装多高的水位

一、三次线性搜索（更简单易懂）

参考wzc1995大佬
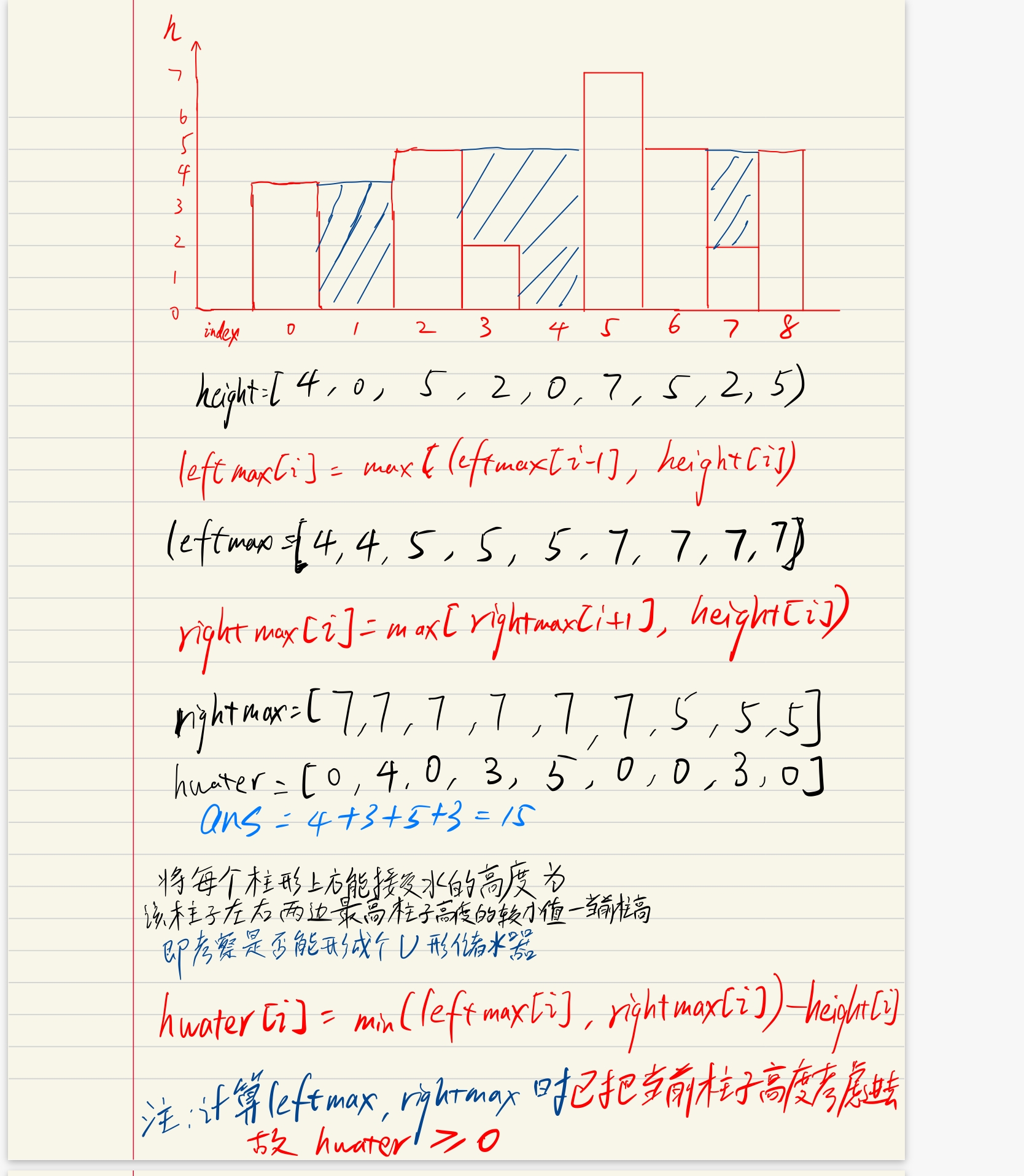
- 第一次：确定每根柱子左边低于等于自己的离自己最近的柱子高度（考虑自己本身，若没有则填入自身高度）
- 第二次：确定每根柱子右边低于等于自己的离自己最近的柱子高度（考虑自己本身，若没有则填入自身高度）
- 第三次：遍历所有柱子上方可储水的高度，加总就是总储水量（柱子宽度为1，所以可忽略不乘上1）

py代码

class Solution:
    def trap(self, height: List[int]) -> int:
        n = len(height)
        ans = 0
        if not n: return 0
        leftmax = [0 for i in range(n)]; rightmax = [0 for i in range(n)] # 存储柱形左右两边的最高柱子的高度（考虑当前柱子本身）
        leftmax[0] = height[0] # 第一个柱子左边最高就是自己本身
        i = 1 
        while i < n:
            leftmax[i] = max(height[i], leftmax[i - 1])
            i += 1

        rightmax[n - 1] = height[n - 1] # 最后一个柱子右边最高就是自己本身
        j = n - 2 
        while j >= 0:
            rightmax[j] = max(height[j], rightmax[j + 1])
            j -= 1
        # 遍历所有柱子上方可储水的高度，加总就是总储水量（柱子宽度为1，所以可忽略不乘上1）
        for i in range(n):
            ans += min(leftmax[i], rightmax[i]) - height[i]

        return ans

二、单调栈

法一

参考wzc1995大佬

py代码

class Solution:
    def trap(self, height: List[int]) -> int:
        res = 0
        stk = []
        for i in range(len(height)):
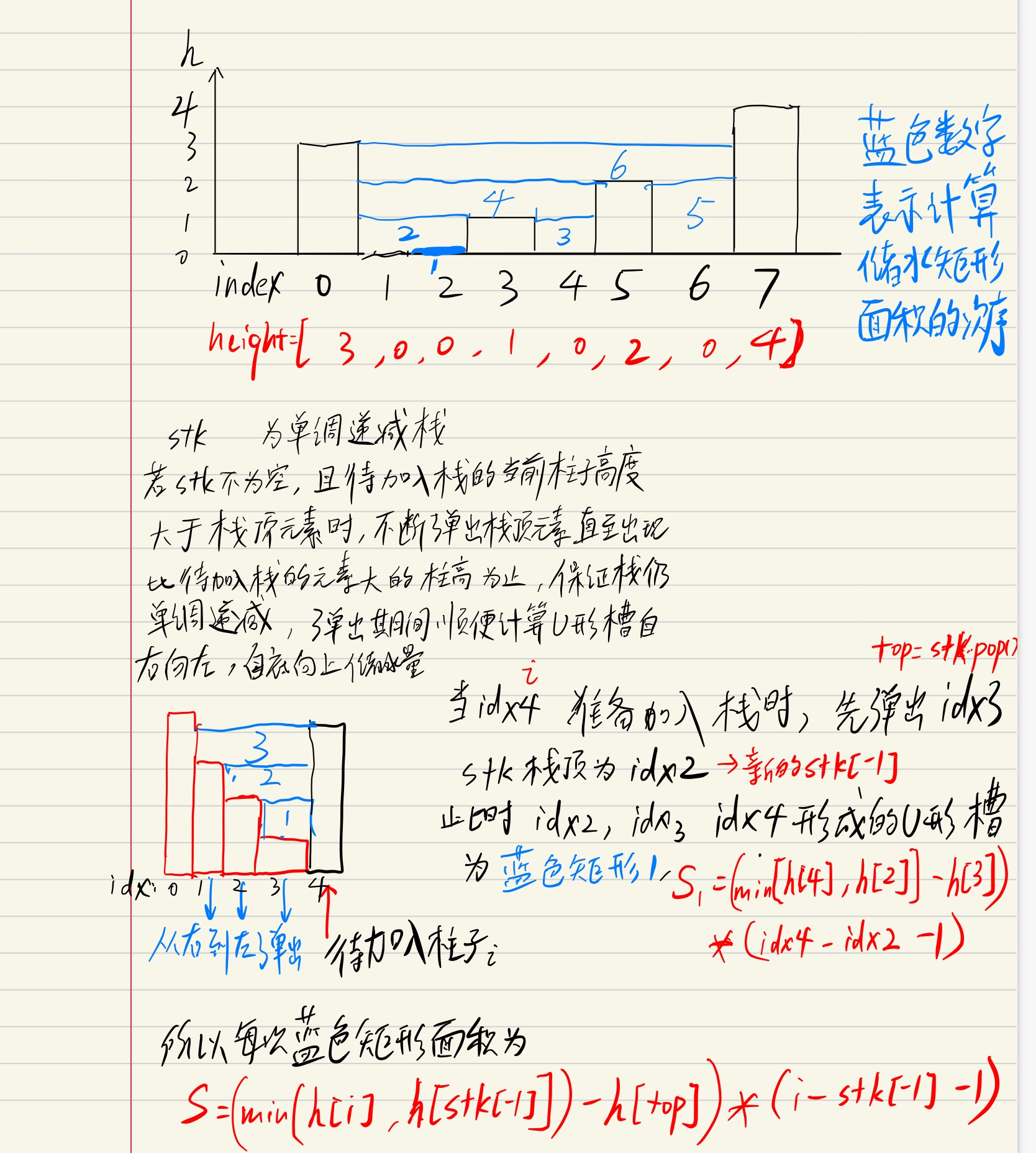
            while len(stk) > 0 and height[stk[-1]] < height[i]:
                top = stk.pop() # U形槽的底部
                if not len(stk): break # 若弹出的是栈中最后一个元素，说明此时不能形成U形槽
                res += (i - stk[-1] - 1) * (min(height[stk[-1]], height[i]) - height[top])
                # min(height[stk[-1]], height)是因为木桶效应，装水的高度取决于木桶最低的木板高度
            stk.append(i)
        return res

法二

参考yxc大佬

py代码

class Solution:
    def trap(self, height: List[int]) -> int:
        res = 0
        stk = []
        i = 0
        while i < len(height):
            bottom = 0 # 新形成的U形槽的底部高度，初始值为0
            while len(stk) > 0 and height[stk[-1]] <= height[i]:# 当栈顶柱子高度小于等于待加入柱子高度
                t = stk.pop() # 删除栈顶元素并存入t

                res += (i - t - 1) * (height[t] - bottom) # 新弹出的柱子高度与上一个弹出的柱子高度之差就是当前U形槽的高度
                # U形槽宽度为待加入柱子与刚弹出柱子之间的柱子数量
                bottom = height[t] # 更新U行槽底部高度为新弹出的柱子高度

            if len(stk) > 0: # 当仍有栈元素未弹出，说明剩余左边柱子比当前待加入柱子高，
                # 则最高的U形槽的高度由待加入柱子高度决定，U形槽高度即为待加入柱子高度-底部高度
                res += (i - stk[-1] - 1) * (height[i] - bottom)
            stk.append(i)  # 将待加入柱子压入栈顶
            i += 1

        return res 
# 单调栈：查找每个数左侧第一个比它小的数
# 单调队列：滑动窗口中的最值