题目描述
汉诺塔问题,条件如下:
1、这里有A、B、C和D四座塔。
2、这里有n个圆盘,n的数量是恒定的。
3、每个圆盘的尺寸都不相同。
4、所有的圆盘在开始时都堆叠在塔A上,且圆盘尺寸从塔顶到塔底逐渐增大。
5、我们需要将所有的圆盘都从塔A转移到塔D上。
6、每次可以移动一个圆盘,当塔为空塔或者塔顶圆盘尺寸大于被移动圆盘时,可将圆盘移至这座塔上。
请你求出将所有圆盘从塔A移动到塔D,所需的最小移动次数是多少。
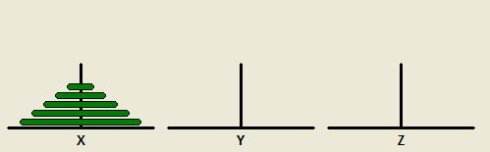
汉诺塔塔参考模型
输入格式
没有输入
输出格式
对于每一个整数n(1≤n≤12),输出一个满足条件的最小移动次数,每个结果占一行。
输入样例:
没有输入
输出样例:
参考输出格式
题解:
先看图:
- 三柱两盘的情况(刨去初时状态,共移动了3次)

- 三柱三盘的情况(刨去初时状态,共移动了7次)

综上两图,我们可以看到,对于n盘3塔问题,移动的最小步数就是,把前n-1个盘子从A柱移到B柱,然后把第n个盘子移到C柱,最后再把前n-1个盘子移动到C柱。可以得出递推式d[n]=d[n−1]∗2+1 。
但是本题没有呢么友善,题目要求我们求四塔情况下最小的移动步数,难受死我了,呢就继续画图看看??
- 四塔3盘(除去初始状态,共移动5次)

- 四塔4盘(除去初始状态,共盘他9次)

综上,可得先把i个盘子在四塔的模式下,移动到一根柱子上(不可以是D柱),然后把n-i个盘子,盘到D柱上。考虑到i可能存在最小值,如上图⑤⑥中的C柱。可得递推式f[i]=min1≤i<n(2∗f[i]+d[n−i]),f[1]=1 。
代码献丑了。。。
#include<bits/stdc++.h>
using namespace std;
int a[15],f[15];
int main(void)
{
a[1] = 1;
for(int i = 2;i <= 12;++i)
a[i] = 1 + a[i-1] * 2;
memset(f,0x3f,sizeof(f));
f[0] = 0;
for(int i = 1;i <= 12;++i)
{
for(int j = 0;j < i;++j)
f[i] = min(f[i],f[j] * 2 + a[i - j]);
}
for(int i = 1;i <= 12;++i)
cout << f[i] << endl;
return 0;
}


没看到图啊
确实电脑端看不到图诶…
min是c++的函数吗,c语言该怎么解
这个 LATEX……
3塔最少移动次数其实等于(2^n-1)次,根据式子也能看出来吧1 3 7 15 31…
memset(f,0x3f,sizeof(f));的0x3f什么意思
1个int的四位全部设为1
讲得不错哦
图看不了🤣
%%%%%
图碎了 大佬