题意：
有n个人,围成一个环，编号为 1、2、3、、、n，从第一个人开始循环报数，假设数到k的那个人出列，然后从下一个人继续数数，数到k出列，以此循环，最后那个人为胜利者，求胜利者的编号。

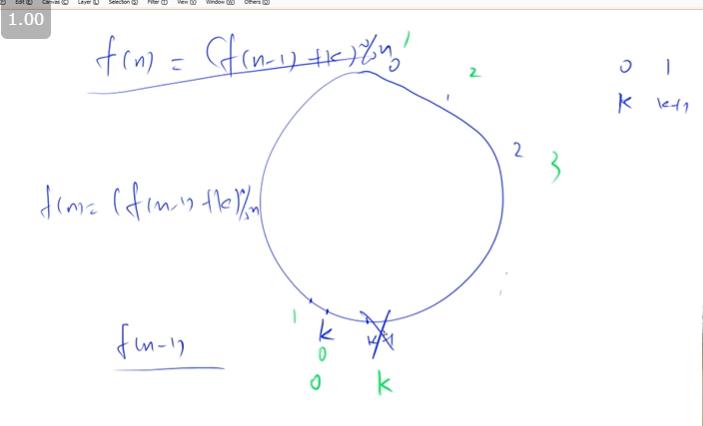
$当数到k-1时的人会出列，那么下一个的编号为k$

$我们进行重新编号，将第k个视为第0个，问题从f(n)变为了f(n-1),只需要加上k的偏移量即可（当前的0是上一轮的k）$

$递推式：f[i]=(f[i-1]+k)%i （其中i是当前有i个人去进行约瑟夫环问题）$

#include<bits/stdc++.h>
using namespace std;

const int N=1e6+10;
int n,k;   
int f[N];

int main(){
    cin>>n>>k;
    f[1]=0;  //第一个猴子下标为0
    for(int i=2;i<=n;i++) f[i]=(f[i-1]+k)%i; 
    cout<<f[n]+1<<endl;  //题目从1开始，所以需要+1
}