思路

对于一个棋盘，先枚举所有横放的长方形，剩余的空间就全部放竖放的长方形
因此可以找出一些限制条件
1. 首先，对于横放的长方形来说，是不可以叠加的，例如在同一列中，两个长方形不能放在（1，2）和（2，3）,对于第二个格子来说，就是叠加，非法的
2. 当讲横放的长方形放好后，对于某一列来说，剩余的连续空白格子，必须都是偶数个，否则会有竖放长方形放不下的情况

因为题目数据小，所以可以将某一列长方形的存放状态用二进制表示

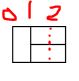
以长方形中间那条线为1，两边的宽为0
则，对于第1列，状态为00(2)
对于第2列，状态为11(2)

针对于上面的两种限制条件

对于第 i 列的状态 j 以及第 i-1 列的状态 k 来说，
1. 如果j&k==1,则表明当前违反了第一种限制条件
2. 如果j|k存在某一段有奇数个0，则表明当前这种状态，会有竖放长方形放不下的情况
3. 故在动态规划过程中，以两个状态满足j&k==0 && st[j|k],其中st是存放当前二进制是否不存在连续奇数个0

C++ 代码

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 12, M = 1 << N;

int n, m;
long long f[N][M];
bool st[M];

int main()
{
    while(cin>>n>> m,n||m)
    {
        memset(f,0,sizeof f);

        //预处理所有状态是否不存在奇数个0
        for(int i=0;i<1<<n; i++){
            st[i]=true;
            int cut=0;//当前连续0的个数
            for(int j=0;j<n;j++){
                if(i>>j&1){//如果遇到1，则连续性被断了，直接判断cnt是否是奇数
                    if(cut&1){
                        st[i]=false;
                        break;
                    }
                    cut=0;
                }
                else cut++;//如果是0，则继续寻找，并且0的数量加1
            }
            if(cut&1) st[i]=false;//判断末尾的情况
        }

        f[0][0]=1;//初始状态是成立的，设为1
        for(int i=1;i<=m;i++){
            for(int j=0;j<1<<n;j++){
                for(int k=0;k<1<<n;k++){
                    if((j&k)==0&&st[j|k])
                        f[i][j]+=f[i-1][k];
                }
            }
        }
        cout<<f[m][0]<<endl;
    }
    return 0;
}