题目描述

你在一家IT公司为大型写字楼或办公楼的计算机数据做备份。

然而数据备份的工作是枯燥乏味的，因此你想设计一个系统让不同的办公楼彼此之间互相备份，而你则坐在家中尽享计算机游戏的乐趣。

已知办公楼都位于同一条街上，你决定给这些办公楼配对（两个一组）。

每一对办公楼可以通过在这两个建筑物之间铺设网络电缆使得它们可以互相备份。

然而，网络电缆的费用很高。

当地电信公司仅能为你提供 K 条网络电缆，这意味着你仅能为 K 对办公楼（总计2K个办公楼）安排备份。

任意一个办公楼都属于唯一的配对组（换句话说，这 2K 个办公楼一定是相异的）。

此外，电信公司需按网络电缆的长度（公里数）收费。

因而，你需要选择这 K 对办公楼使得电缆的总长度尽可能短。

换句话说，你需要选择这 K 对办公楼，使得每一对办公楼之间的距离之和（总距离）尽可能小。

下面给出一个示例，假定你有 5 个客户，其办公楼都在一条街上，如下图所示。

这 5 个办公楼分别位于距离大街起点 1km, 3km, 4km, 6km 和 12km 处。

电信公司仅为你提供 K=2 条电缆。

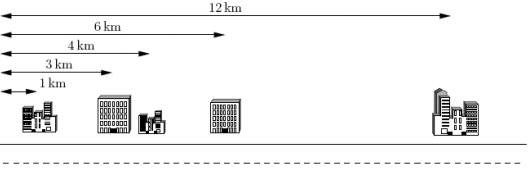
上例中最好的配对方案是将第 1 个和第 2 个办公楼相连，第 3 个和第 4 个办公楼相连。

这样可按要求使用 K=2 条电缆。

第 1 条电缆的长度是 3km-1km=2km ，第 2 条电缆的长度是 6km-4km=2km。

这种配对方案需要总长 4km 的网络电缆，满足距离之和最小的要求。

输入格式
第一行输入整数n和k，其中 n 表示办公楼的数目，k 表示可利用的网络电缆的数目。

接下来的n行每行仅包含一个整数s,表示每个办公楼到大街起点处的距离。

这些整数将按照从小到大的顺序依次出现。

输出格式
输出应由一个正整数组成，给出将2K个相异的办公楼连成k对所需的网络电缆的最小总长度。

数据范围
$2≤n≤100000$
$1≤k≤n/2$
$0≤s≤1000000000$

样例

输入样例：
5 2 
1
3
4
6
12
输出样例：
4

优先队列(堆)+贪心+链表

这道题目我们首先很容易发现性质,最优解中每两个配对的办公楼一定是相邻的,既然如此的话不妨设置一个数组D,D[i]表示第i个办公楼和第i-1个办公楼之前的距离.然后我们发现,如果说当前D数组中最小值为D[i],那么会有两种情况产生.

1. 选择了D[i],那么D[i-1]和D[i+1]都不能选择了
2. 选择了D[i+1]和D[i-1],然后无法选择D[i].

分析上面两个方案,我们发现这是唯一的两个方案,也就是最优解,最小值的左右两侧的数,要么都选择,要么都不选择.

既然如此的话,我们可以可以先选则D数列中的最小值,然后把D[i-1],D[i],D[i+1]从D数列中删除,然后我们再在这个位置插入D[i-1]+D[i+1]-D[i]也就是说,选择左右两个位置不选择D[i]这种方案,于是这样,我们就成功的让这两个方案都加入到了优先队列之中.

至于如何维护这个位置的话,我们可以使用专门维护前驱和后继的链表.

C++ 代码

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inf 0x3f3f3f3f
#define N 100010
inline int read()//快速读入
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
    return x*f;
}
int n,K,a[N],pre[N],nxt[N];
bool del[N];
ll ans=0;
struct cmp
{
    bool operator()(int x,int y)//最小排序
    {
        return a[x]>a[y];
    }
};
priority_queue<int,vector<int>,cmp>q;
int main()
{
    n=read();
    K=read();
    a[1]=read();
    for(int i=2; i<=n; i++) 
        a[i]=read(),a[i-1]=a[i]-a[i-1];//开始计算权值
    n--;
    a[0]=inf;
    for(int i=1; i<=n; i++) 
        q.push(i),pre[i]=i-1,nxt[i]=i+1>n?0:i+1;//设置前驱后继.
    while(K--)
    {
        int x=q.top();//第一种方案
        q.pop();
        while(del[x])
        {
            x=q.top();
            q.pop();
        }
        ans+=a[x];//加上消耗的长度
        del[pre[x]]=1;
        del[nxt[x]]=1;
        a[x]=a[pre[x]]+a[nxt[x]]-a[x];//开始使用第二种方案
        q.push(x);
        pre[x]=pre[pre[x]];
        nxt[x]=nxt[nxt[x]];
        nxt[pre[x]]=x;
        pre[nxt[x]]=x;
        //更新前驱和后继
    }
    cout<<ans;
    return 0;
}