题目描述

给定两个闭区间的链表，每个链表中的区间都是相互不重叠的，并且都是升序排列。

返回两个区间链表的交集链表。

（正式地，一个闭区间 [a, b] (a <= b) 表示一个集合，其中的实数 x 满足 a <= x <= b。两个闭区间的交集是一个空集，或者是另一个闭区间。例如，[1, 3] 和 [2, 4] 的交集是 [2, 3]。

样例

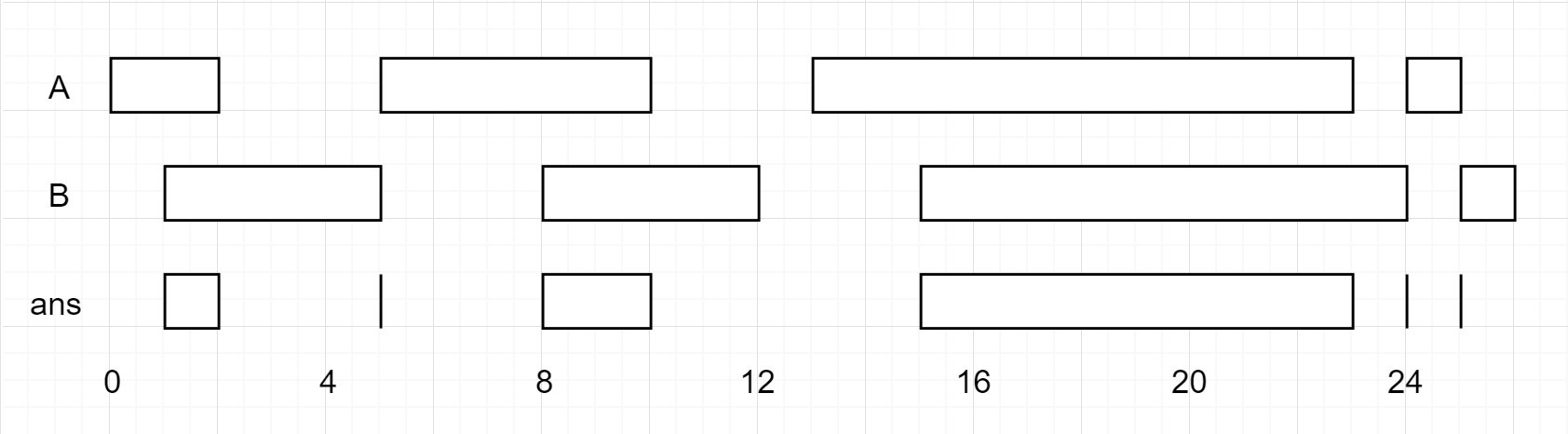
输入：A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
输出：[[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
提醒：输入和期望的输出都是 Interval 对象的链表，不是数组或者 list 链表。

注意

• 0 <= A.length < 1000
• 0 <= B.length < 1000
• 0 <= A[i].start, A[i].end, B[i].start, B[i].end < 10^9

算法

(模拟) $O(n + m)$

1. 分类讨论：假设 A 中当前线段的左右端点是 s1 和 e1，B 中当前线段的左右端点是 s2 和 e2。
2. 若 s1 <= s2，则如果 e1 < s2，说明 B 中的线段已经完全在 A 线段的右侧，则直接考察 A 的下一个线段；否则，这里一定会出现线段相交，相交的部分为 [s2, min(e1, e2)]，这时还需要继续分类，若 e1 >= e2，说明 A 的线段完全覆盖了 B 的线段，此时应该考察 B 的下一个线段；否则，需要考察 A 的下一个线段。
3. 若 s1 < s2，则处理方式相似。
4. 直到某个列表走完为止。

时间复杂度

• 每条线段最多遍历一次，故时间复杂度为 $O(n + m)$。

空间复杂度

• 需要记录答案的数组，故空间复杂度也为 $O(n + m)$。

C++ 代码

/**
 * Definition for an interval.
 * struct Interval {
 *     int start;
 *     int end;
 *     Interval() : start(0), end(0) {}
 *     Interval(int s, int e) : start(s), end(e) {}
 * };
 */
class Solution {
public:
    vector<Interval> intervalIntersection(vector<Interval>& A, vector<Interval>& B) {
        int n = A.size(), m = B.size();
        vector<Interval> ans;
        int i = 0, j = 0;
        while (i < n && j < m) {
            int s1 = A[i].start, e1 = A[i].end;
            int s2 = B[j].start, e2 = B[j].end;
            if (s1 <= s2) {
                if (e1 < s2) {
                    i++;
                }
                else {
                    ans.emplace_back(Interval(s2, min(e1, e2)));
                    if (e1 >= e2) {
                        j++;
                    } else {
                        i++;
                    }
                }
            }
            else {
                if (e2 < s1) {
                    j++;
                }
                else {
                    ans.emplace_back(Interval(s1, min(e1, e2)));
                    if (e1 <= e2) {
                        i++;
                    } else {
                        j++;
                    }
                }
            }
        }
        return ans;
    }
};