题目描述

给定一棵二叉树，返回结点值的垂直顺序遍历

对于每个在位置 (X, Y) 的结点，左儿子和右儿子的位置可以分别表示为 (X-1, Y-1) 和 (X+1, Y-1)。

从 X = -infinity 到 X = +infinity 运行一条竖直线，当这条线触碰到了某些结点，我们按照从顶到底的顺序汇报结点的值。（Y 坐标的降序排列）。

如果两个结点有相同的位置，则汇报的顺序按照结点的值从小到大。

按 X 坐标的顺序返回一个非空的汇报列表，每一次汇报都是一个结点值的列表。

样例

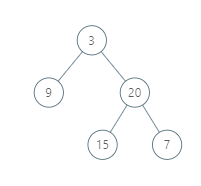
输入：[3,9,20,null,null,15,7]
输出：[[9],[3,15],[20],[7]]
解释：
不失一般性，我们假定根结点在位置 (0, 0)：
然后，结点 9 在位置 (-1, -1)；
结点 3 和 15 在位置 (0, 0) 和 (0, -2)；
结点 20 在位置 (1, -1)；
结点 7 在位置 (2, -2)。

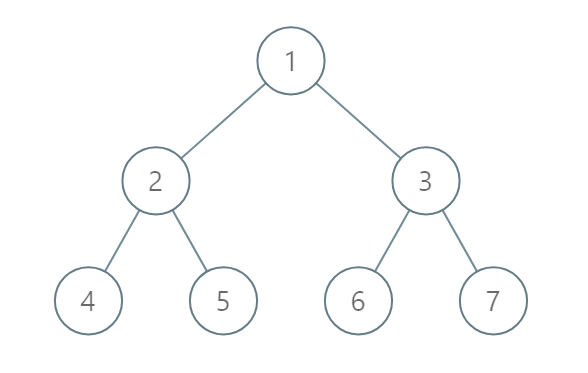
输入：[1,2,3,4,5,6,7]
输出：[[4],[2],[1,5,6],[3],[7]]
解释：
结点 5 和结点 6 有相同的位置。
然而，在报告 "[1,5,6]" 中，结点 5 比结点 6 靠前因为 5 小于 6。

算法

(深度优先遍历) $O(n \log n)$

1. 通过一个 (x, y) 到 vector<int> 的映射，通过深度优先遍历记录每个位置存的结点的值。
2. C++ 的 map 会自动按照 x 从小到大排序，其中 x 相等的会按照 y 从小到大排序。
3. 然后逐一遍历 map 中的值，如果当前的 x 值与上一次不一致，则新开一个数组。否则，将当前的 vector 排序后加入当前答案数组的末尾。

时间复杂度

• 总共 $n$ 个结点，插入结点到映射中需要 $O(\log n)$ 的时间，统计答案需要部分排序，需要 $O(n \log n)$ 的时间，故总时间复杂度为 $O(n \log n)$。

空间复杂度

• 递归遍历需要 $O(h)$ 的栈空间，map 映射需要 $O(n)$ 的空间，最终答案也需要 $O(n)$ 的空间，故总空间复杂度为 $O(n)$。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:

    void dfs(TreeNode *rt, int x, int y, map<pair<int, int>, vector<int>> &nodes) {
        nodes[make_pair(x, y)].push_back(rt -> val);
        if (rt -> left != nullptr)
            dfs(rt -> left, x - 1, y + 1, nodes);
        if (rt -> right != nullptr)
            dfs(rt -> right, x + 1, y + 1, nodes);
    }

    vector<vector<int>> verticalTraversal(TreeNode* root) {
        map<pair<int, int>, vector<int>> nodes;
        dfs(root, 0, 0, nodes);
        vector<vector<int>> ans;
        int last_x = -10000;
        for (auto pr : nodes) {
            int x = pr.first.first;
            vector<int> tmp(pr.second);
            sort(tmp.begin(), tmp.end());
            if (x != last_x) {
                ans.push_back(tmp);
            }
            else {
                for (int j = 0; j < tmp.size(); j++)
                    ans[ans.size() - 1].push_back(tmp[j]);
            }
            last_x = x;
        }
        return ans;
    }
};