题目描述

给定一棵二叉树的根结点 root，每个结点的值都在 0 到 25 之间表示字母 'a' 到 'z'：结点值为 0 表示 'a'，结点值为 1 表示 'b'，以此类推。

找到字典序最小的字符串，字符串从叶结点开始，到根结点结束。

（提醒，一个字符串的任何较短的前缀都是字典序小于它本身的：例如，"ab" 字典序小于 "aba"。叶结点是没有儿子的结点。）

样例

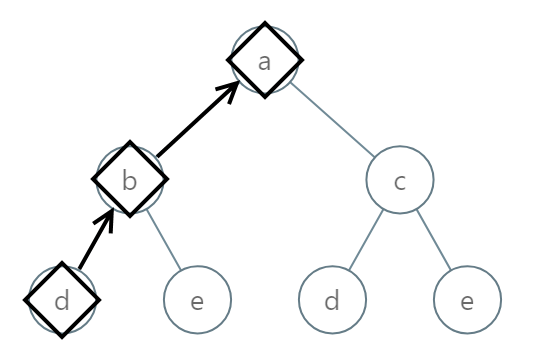
输入：[0,1,2,3,4,3,4]
输出："dba"

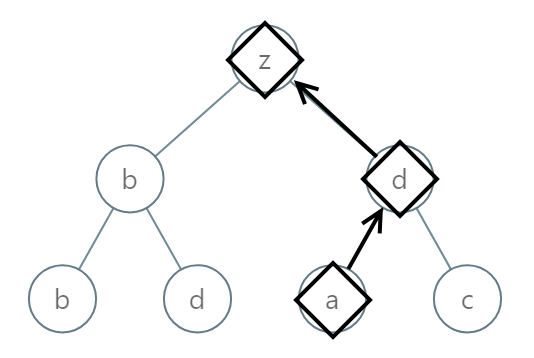
输入：[25,1,3,1,3,0,2]
输出："adz"

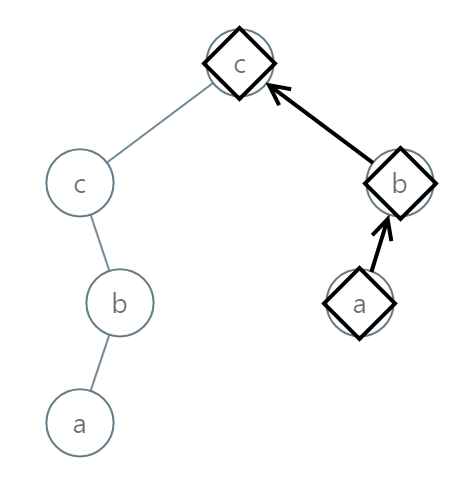
输入：[2,2,1,null,1,0,null,0]
输出："abc"

注意

• 给定树的结点个数在 1 到 1000 之间。
• 每个结点值都在 0 到 25 之间。

算法

(暴力枚举，深度优先遍历) $O(n)$

1. 直接从根结点开始深度优先遍历，遍历过程中记录字符串。
2. 最后到叶结点后，将记录的字符串反向，然后更新答案。

时间复杂度

• 每个结点最多遍历一次，故时间复杂度为 $O(n)$。

空间复杂度

• 遍历过程中需要字符串记录，这里需要 $O(h)$ 的空间。
• 递归的栈也需要 $O(h)$ 的空间。
• 故总空间复杂度为 $O(h)$，其中 $h$ 表示树的最大深度。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:

    void dfs(TreeNode *rt, string &cur, string &ans) {
        cur += (char)(rt -> val + 'a');
        if (rt -> left == nullptr && rt -> right == nullptr) {
            reverse(cur.begin(), cur.end());
            if (ans == "" || ans > cur)
                ans = cur;
            reverse(cur.begin(), cur.end());
            cur.pop_back();
            return;
        }
        if (rt -> left != nullptr)
            dfs(rt -> left, cur, ans);
        if (rt -> right != nullptr)
            dfs(rt -> right, cur, ans);
        cur.pop_back();
    }

    string smallestFromLeaf(TreeNode* root) {
        string ans = "", cur;
        dfs(root, cur, ans);
        return ans;
    }
};