题目描述

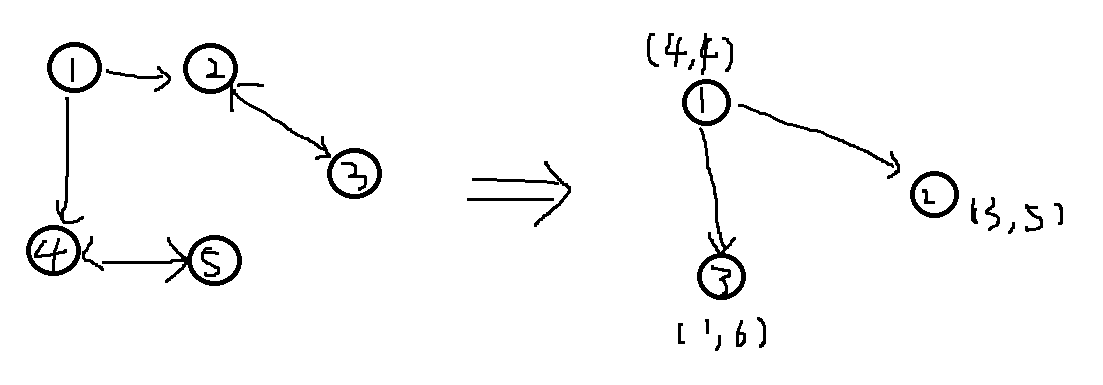
题目说，从点1到点n，期间可以任意次数拜访任意城市。

如上图，从样例我们可以看出，一个强连通图中信息是共享的（任意点之间相互可以拜访），那我们不如先用tarjan缩点，使得图变成DAG（有向无环图），容易知道，一个缩点的信息我们只需要留下最大值和最小值即可。这样图的性质变简单了，也存下了连通图中的任意拜访的上下界数值。

当然，我们需要从整个图中截取一个有效的子图，因为我们只需要从1 ->中间其他点 -> n。
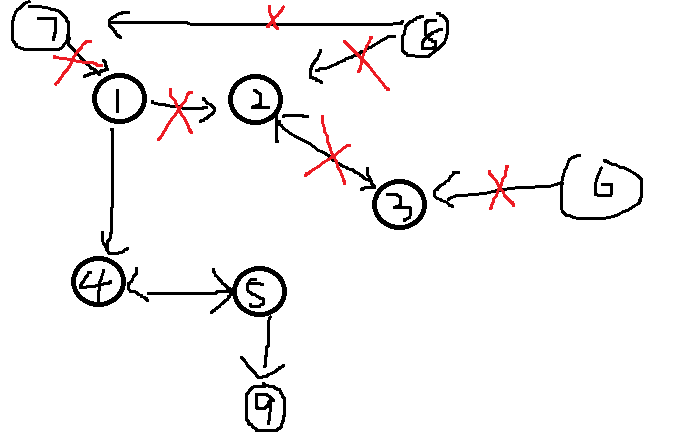
所以我们要从缩点之后的图中，从点1所处的scc向其他可以到达的scc跑，其他跑不到的点都是无用的信息，我们需要记录那些可以到达的scc，从上图看出，当我们得到了有效图的时候，其实这个图是以点1所在的scc为出发点的拓扑图，这样我们用拓扑排序来传递信息就可以了。

如下图：红色即为无用信息

$O(m)$

时间复杂度

tarjan一次O(m)，dfs一次O（m），拓扑排序O（m），其他复杂度基本都是遍历所有边。

C++ 代码

代码挺长的，如果熟悉这些算法，也就是码量多一点，处理起来不难。

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <queue>

using namespace std;

#define pb push_back
#define fi first
#define se second

const int N = 1e5 + 10;
vector<int > E[N], SCC[N], new_E[N];
pair<int ,int > range[N];
int dfn[N], low[N], ins[N], id[N], s[N], v[N], ru[N], vis[N], go[N];
int n, m, tim, top, col;

//trajan缩点
void Tarjan(int now, int pre)
{
    dfn[now] = low[now] = ++tim;
    ins[now] = 1; s[top++] = now;

    for(auto to : E[now]) {
        if(!dfn[to]) {
            Tarjan(to, now);    
            low[now] = min(low[now], low[to]);
        } else if(ins[to]) {
            low[now] = min(low[now], dfn[to]);
        }
    }

    if(dfn[now] == low[now]) {
        ++col;
        while(1) {
            int tmp = s[--top];
            ins[tmp] = 0;
            SCC[col].pb(tmp);
            id[tmp] = col;
            if(tmp == now) break;
        }
    }
}

int dfs(int now)
{
    if(now ==  id[n]) {
        go[now] = 1;
        return 1;
    }

    vis[now] = 1;
    int Find = 0;
    for(auto to : new_E[now]) {
        if(vis[to]) continue;
        Find += dfs(to);
    }
    if(Find) go[now] = 1;
    return Find;
}

//建新图
void Build()
{
    //for(int i = 1; i <= n; ++i) printf("col[%d] = %d\n", i, id[i]);
    for(int now = 1; now <= n; ++now) {
        for(auto to : E[now]) {
            if(id[now] == id[to]) continue;
            new_E[id[now]].pb(id[to]);
        }
    }
    //处理有效图 go[x] = true 表示有效点
    dfs(id[1]);
    /*
    for(int i = 1; i <= col; ++i) {
        if(go[i]) {
            printf("%d is lighted\n", i);
        }
    }*/

    for(int now = 1; now <= n; ++now) {
        for(auto to : E[now]) {
            int x = id[now];
            int y = id[to];
            //是不是都是有效点  是不是处于同一个scc
            if(!go[x] || !go[y] || x == y) continue;
            //拓扑序处理
            ru[y]++;
        }
    }
}

int Top_sort()
{
    //for(int i = 1; i <= col; ++i) if(go[i]) cout << ru[i] << endl;
    queue<int > que;
    //从点1的scc出发处理拓扑图
    que.push(id[1]);

    int ans = 0;
    while(!que.empty()) {
        int now = que.front();
        que.pop();

        for(auto to : new_E[now]) {
            if(!go[to]) continue;
            //传递信息
            range[to].fi = min(range[to].fi, range[now].fi);

           //该点已经无法在得到其他点的信息
            if(--ru[to] == 0) {
                //更新答案
                ans = max(ans, range[to].se - range[to].fi);
                que.push(to);
            } 
        }
    }

    return ans;
}

void solve()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; ++i) scanf("%d", v + i);
    for(int i = 1; i <= m; ++i) {
        int u, v, op;
        scanf("%d%d%d", &u, &v, &op);
        E[u].pb(v);
        if(op == 2) {
            E[v].pb(u);
        }
    }

    for(int i = 1; i <= n; ++i) {
        if(!dfn[i]) {
            Tarjan(i, i);
        }
    }    

    for(int i = 1; i <= col; ++i) {
        int Min = 1e9;
        int Max = -1e9;
        for(auto x : SCC[i]) {
            Min = min(Min, v[x]);
            Max = max(Max, v[x]);
        }
        //得到一个scc的上下界价格
        range[i] = make_pair(Min, Max);
       // cout << range[i].fi <<" "<<range[i].se<<endl;
    }

    Build();

    printf("%d\n", Top_sort());

}

int main()
{
    solve();

    return 0;
}

上面的方法多余处理些内容，我们发现，当我们tarjan后，我们可以直接dfs以点1所在的scc跑新图，并且更新跑到点的信息，如果dfs到了点n所在的scc中，我们就更新答案。我们需要vis[]数组标记访问过的scc，因为一个scc到另一个scc可能有很多条边，防止scc之间的边重复跑。

C++ 代码

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <queue>

using namespace std;

#define pb push_back
#define fi first
#define se second

const int N = 1e5 + 10;
vector<int > E[N], SCC[N], new_E[N];
pair<int ,int > range[N];
int dfn[N], low[N], ins[N], id[N], s[N], v[N], ru[N], vis[N], go[N];
int n, m, tim, top, col;

//trajan缩点
void Tarjan(int now, int pre)
{
    dfn[now] = low[now] = ++tim;
    ins[now] = 1; s[top++] = now;

    for(auto to : E[now]) {
        if(!dfn[to]) {
            Tarjan(to, now);    
            low[now] = min(low[now], low[to]);
        } else if(ins[to]) {
            low[now] = min(low[now], dfn[to]);
        }
    }

    if(dfn[now] == low[now]) {
        ++col;
        while(1) {
            int tmp = s[--top];
            ins[tmp] = 0;
            SCC[col].pb(tmp);
            id[tmp] = col;
            if(tmp == now) break;
        }
    }
}

//建新图
void Build()
{
    //for(int i = 1; i <= n; ++i) printf("col[%d] = %d\n", i, id[i]);
    for(int now = 1; now <= n; ++now) {
        for(auto to : E[now]) {
            if(id[now] == id[to]) continue;
            new_E[id[now]].pb(id[to]);
        }
    }
}


void dfs(int now, int gap, int& ans)
{

    gap = max(gap, range[now].se - range[now].fi);
    //跑到了n所处的scc，更新答案
    if(now == id[n]) {
        //cout << "in " << endl;
        ans = max(ans, gap);
        return ;
    }
    vis[now] = 1;
    for(auto to : new_E[now]) {
        if(vis[to]) continue;
        //更新信息
        range[to].fi = min(range[to].fi, range[now].fi);
        dfs(to, gap, ans);
    }
}

void solve()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; ++i) scanf("%d", v + i);
    for(int i = 1; i <= m; ++i) {
        int u, v, op;
        scanf("%d%d%d", &u, &v, &op);
        E[u].pb(v);
        if(op == 2) {
            E[v].pb(u);
        }
    }

    for(int i = 1; i <= n; ++i) {
        if(!dfn[i]) {
            Tarjan(i, i);
        }
    }    

    for(int i = 1; i <= col; ++i) {
        int Min = 1e9;
        int Max = -1e9;
        for(auto x : SCC[i]) {
            Min = min(Min, v[x]);
            Max = max(Max, v[x]);
        }
        //得到一个scc的上下界价格
        range[i] = make_pair(Min, Max);
       // cout << range[i].fi <<" "<<range[i].se<<endl;
    }

    Build();
    int ans = 0;
    dfs(id[1], 0, ans);

    printf("%d\n", ans);

}

int main()
{
    solve();
    //cout << "ok" << endl;
    return 0;
}