题目描述
小城和小华都是热爱数学的好学生,最近,他们不约而同地迷上了数独游戏,好胜的他们想用数独来一比高低。
但普通的数独对他们来说都过于简单了,于是他们向Z博士请教,Z博士拿出了他最近发明的“靶形数独”,作为这两个孩子比试的题目。
靶形数独的方格同普通数独一样,在9×9的大九宫格中有9个3×3的小九宫格(用粗黑色线隔开的)。
在这个大九宫格中,有一些数字是已知的,根据这些数字,利用逻辑推理,在其他的空格上填入1到9的数字。
每个数字在每个小九宫格内不能重复出现,每个数字在每行、每列也不能重复出现。
但靶形数独有一点和普通数独不同,即每一个方格都有一个分值,而且如同一个靶子一样,离中心越近则分值越高(如下图所示)。
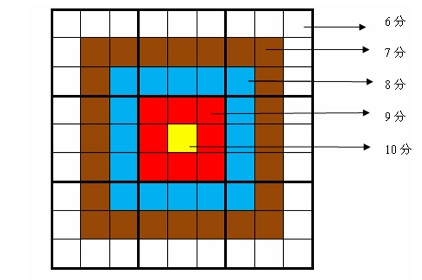
上图具体的分值分布是:最里面一格(黄色区域)为10分,黄色区域外面的一圈(红色区域)每个格子为9分,再外面一圈(蓝色区域)每个格子为8分,蓝色区域外面一圈(棕色区域)每个格子为7分,最外面一圈(白色区域)每个格子为6 分,如上图所示。
比赛的要求是:每个人必须完成一个给定的数独(每个给定数独可能有不同的填法),而且要争取更高的总分数。
而这个总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和。
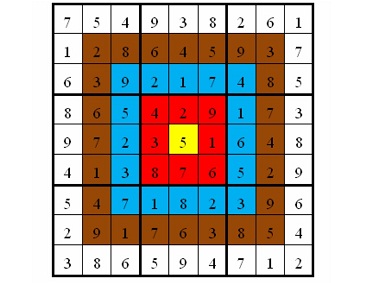
如图,在以下的这个已经填完数字的靶形数独游戏中,总分数为2829。
游戏规定,将以总分数的高低决出胜负。
由于求胜心切,小城找到了善于编程的你,让你帮他求出,对于给定的靶形数独,能够得到的最高分数。
输入格式
输入一共包含9行。
每行 9 个整数(每个数都在 0—9 的范围内),表示一个尚未填满的数独方格,未填的空格用“0”表示。
每两个数字之间用一个空格隔开。
输出格式
输出可以得到的靶形数独的最高分数。
如果这个数独无解,则输出整数-1。
数据范围
40的数据,数独中非 0 数的个数不少于 30。
80的数据,数独中非 0 数的个数不少于 26。
100的数据,数独中非 0 数的个数不少于 24。
样例
输入样例:
7 0 0 9 0 0 0 0 1
1 0 0 0 0 5 9 0 0
0 0 0 2 0 0 0 8 0
0 0 5 0 2 0 0 0 3
0 0 0 0 0 0 6 4 8
4 1 3 0 0 0 0 0 0
0 0 7 0 0 2 0 9 0
2 0 1 0 6 0 8 0 4
0 8 0 5 0 4 0 1 2
输出样例:
2829
搜索+剪枝+卡常
这道题目满分做法是:每一次找到可填数字最小的位置填数,然后位运算常数优化这个位置可不可以填写,用lowbit找出可以填写的数字,这个方法代码量特长,而且极为难做.
下面是95分简短做法+5分手动数据怒对出题人 codevs满分,Luogu 95分,vijos 95分(没有手动数据的情况下)
优化搜索顺序:我们可以直接倒着搜索枚举,不要问我为什么,这就是出题人用心险恶.
可行化剪枝:如果当前值加上剩下的空*64(八八六十四)(其实81(九九八十一)最稳妥,但是常数优化)的值还小于我们找到的当前最优解,那么可以剪掉.
C++ 代码
#include<cstdio>
#include<ctime>
#pragma GCC optimize(3)//手动O3
#pragma G++ optimize(3)//手动O3
#define Next(x,y) (y)==9? dfs((x)+1,1):dfs((x),(y)+1)//搜索下一个位置
#define del(x,y,k) b[(x)][(y)]=r[(x)][(k)]=l[(y)][(k)]=s[pd((x),(y))][(k)]=0//没有访问
#define max(a,b) (a)>(b)?(a):(b)//求两个数字中的最大值
const int N=10;
bool r[N][N],l[N][N],s[N][N];
int ns[N][N][N],a[N][N],b[N][N];
int ans=-1,now_ans,last_ans;
inline int pd(int x,int y)
{
return (x-1)/3*3+(y-1)/3+1;//处理行和列
}
inline int rc(int x,int y,int k)//监测权值
{
if(x==5 && y==5)
return 10*k;
else if(x>=4 && x<=6 && y>=4 && y<=6)
return 9*k;
else if(x>=3 && x<=7 && y>=3 && y<=7)
return 8*k;
else if(x>=2 && x<=8 && y>=2 && y<=8)
return 7*k;
else
return 6*k;
}
inline bool check(int x,int y,int k)
{
if(r[x][k])
return 0;
if(l[y][k])
return 0;
if(s[pd(x,y)][k])
return 0;
b[x][y]=k;
r[x][k]=l[y][k]=s[pd(x,y)][k]=1;
now_ans+=ns[x][y][k];
return 1;
}
inline void dfs(int x,int y)
{
if(x==10 && y==1)
{
ans=max(ans,now_ans);
return ;
}
if (now_ans+64*last_ans<=ans)//优秀的剪枝,如果发现当前值加上剩余的数的极大值,还是小于我们找到的答案,那么可以剪枝剪掉了.
return ;
if(b[x][y])//如果这个位置已经被填好了数值.
{
Next(x,y);
return ;
}
else
{
for(int i=9; i>=1; i--)//开始枚举
{
int t=now_ans;
if(check(x,y,i))//如果这个数字可以填上去.
{
last_ans--;
Next(x,y);
del(x,y,i);
now_ans=t;
last_ans++;
}
}
}
}
int main()
{
for(int i=1; i<=9; i++)
for(int j=1; j<=9; j++)
for(int k=1; k<=9; k++)
ns[i][j][k]=rc(i,j,k);//任意一个位置(i,j)放任意一个数字k的权值
for(int i=9; i>0; i--)
for(int j=9; j>0; j--)
{
scanf("%d",&a[i][j]);
if(a[i][j])
check(i,j,a[i][j]);
else
last_ans++;//统计有多少个空
}
if (a[9][9]==1 && a[1][1]==4)//苦酒入喉,手动砍数据,大吼一声:出题人丧心病狂
{
printf("2852\n");
return 0;
}
dfs(1,1);
printf("%d",ans);
return 0;
}
以下为lyd金牌爷光盘上完美做法
// Author: Rose_max
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
const int ptm[11][11]=
{
{0,0,0,0,0,0,0,0,0,0},
{0,6,6,6,6,6,6,6,6,6},
{0,6,7,7,7,7,7,7,7,6},
{0,6,7,8,8,8,8,8,7,6},
{0,6,7,8,9,9,9,8,7,6},
{0,6,7,8,9,10,9,8,7,6},
{0,6,7,8,9,9,9,8,7,6},
{0,6,7,8,8,8,8,8,7,6},
{0,6,7,7,7,7,7,7,7,6},
{0,6,6,6,6,6,6,6,6,6}
};//直接上地图
int bin[25],sum,ans;
int mp[15][15];
int row[15],col[15],po[15];
int G(int x,int y)
{
return (x-1)/3*3+(y-1)/3+1;
}
void dfs(int k,int pt)
{
if(k==sum+1)
{
ans=max(ans,pt);
return ;
}
int u,v,s=999999999,gu;
for(int i=1; i<=9; i++)
for(int j=1; j<=9; j++)
if(!mp[i][j])
{
int tmp=row[i]&col[j]&po[G(i,j)],ret=0;//如果可以填写
if(tmp==0)return ;
for(int k=1; k<=9; k++)if(tmp&bin[k])ret++;
if(ret<s)u=i,v=j,s=ret,gu=tmp;
}
if(ptm[u][v]<=7)//还是挺玄学的emm
{
for(int i=1; i<=9; i++)
if(gu&bin[i])
{
mp[u][v]=i;
row[u]^=bin[i];
col[v]^=bin[i];
po[G(u,v)]^=bin[i];
dfs(k+1,pt+i*ptm[u][v]);
mp[u][v]=0;
row[u]|=bin[i];
col[v]|=bin[i];
po[G(u,v)]|=bin[i];
}
}
else
{
for(int i=9; i>=1; i--)
if(gu&bin[i])
{
mp[u][v]=i;
row[u]^=bin[i];
col[v]^=bin[i];
po[G(u,v)]^=bin[i];
dfs(k+1,pt+i*ptm[u][v]);
mp[u][v]=0;
row[u]|=bin[i];
col[v]|=bin[i];
po[G(u,v)]|=bin[i];
}
}
}
int main()
{
bin[1]=1;
for(int i=2; i<=20; i++)bin[i]=bin[i-1]<<1;
for(int i=1; i<=9; i++)for(int j=1; j<=9; j++)scanf("%d",&mp[i][j]);
for(int i=1; i<=9; i++)row[i]=col[i]=po[i]=(1<<9)-1;
bool bk=false;
int p=0;
for(int i=1; i<=9; i++)for(int j=1; j<=9; j++)
{
if(mp[i][j])
{
if(row[i]&bin[mp[i][j]])row[i]^=bin[mp[i][j]];
else
{
bk=true;
break;
}
if(col[j]&bin[mp[i][j]])col[j]^=bin[mp[i][j]];
else
{
bk=true;
break;
}
int tmp=G(i,j);
if(po[tmp]&bin[mp[i][j]])po[tmp]^=bin[mp[i][j]];
else
{
bk=true;
break;
}
p+=mp[i][j]*ptm[i][j];
}
else sum++;
}
if(bk)
{
printf("-1\n");
return 0;
}
ans=-1;
dfs(1,0);
if(ans==-1)printf("-1\n");
else printf("%d\n",ans+p);
return 0;
}


手动砍数据真的强哈哈