题目描述

房间中有 n 枚灯泡，编号从 1 到 n，自左向右排成一排。最初，所有的灯都是关着的。

在 k 时刻（k 的取值范围是 0 到 n - 1），我们打开 light[k] 这个灯。

一个灯的颜色 变成蓝色 当且仅当它处于打开状态，且排在它之前（左侧）的所有灯也都处于打开状态。

请返回能够让 所有开着的 灯都 变成蓝色 的时刻数目。

样例

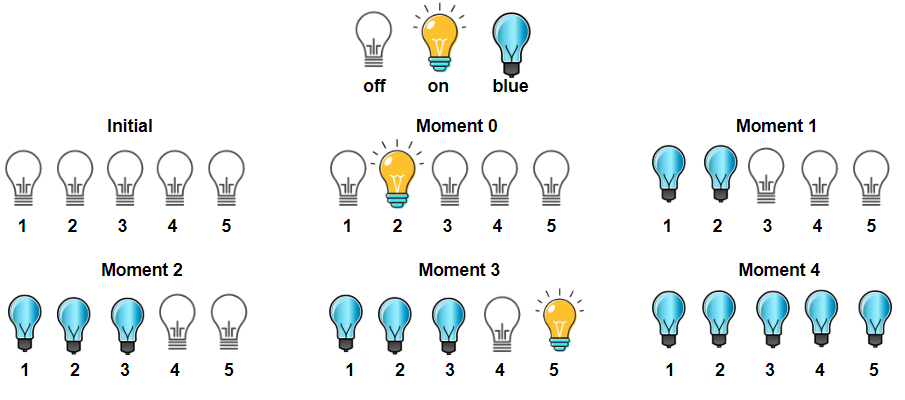
输入：light = [2,1,3,5,4]
输出：3
解释：所有开着的灯都变蓝的时刻分别是 1，2 和 4。

输入：light = [3,2,4,1,5]
输出：2
解释：所有开着的灯都变蓝的时刻分别是 3 和 4（index-0）。

输入：light = [4,1,2,3]
输出：1
解释：所有开着的灯都变蓝的时刻是 3（index-0）。
第 4 个灯在时刻 3 变蓝。

输入：light = [2,1,4,3,6,5]
输出：3

输入：light = [1,2,3,4,5,6]
输出：6

限制

• n == light.length
• 1 <= n <= 5 * 10^4
• light 是 [1, 2, ..., n] 的一个排列。

算法

(找规律) $O(n)$

1. 我们每次记录下开着的编号最大的灯，如果这个编号等于所有已经开着的灯的数量，则这个时刻灯必定是全是蓝色的。
2. 所以只需要按顺序扫描每个时刻，然后维护最大编号。

时间复杂度

• 线性扫描，故时间复杂度为 $O(n)$。

空间复杂度

• 仅需要常数的额外空间。

C++ 代码

class Solution {
public:
    int numTimesAllBlue(vector<int>& light) {
        int n = light.size();

        int max_light = 0, ans = 0;
        for (int i = 0; i < n; i++) {
            max_light = max(max_light, light[i]);
            if (i + 1 == max_light)
                ans++;
        }

        return ans;
    }
};